#10 Hyperbolická regrese

Vrhneme se na hyperbolickou regresi... "Proč, proboha, na hyperbolickou regresi?!" říkáš si asi teď. Tak ještě jednou, pro zopakování. Regresní analýza je základní zpětnovazebný mechanizmus strojového učení a potažmo v obecné rovině umělé inteligence. Čím širší spektrum regresí budeš znát a umět je naprogramovat, tím flexibilněji budeš moct realizovat úlohy, které bude mět tvoje AI řešit. Nikdy dopředu nevíš, jaká regrese se ti bude hodit a ani já ti to teď neřeknu. Protože nevím, jaké úlohy budeš kdy řešit (vždy je strojové učení zatím vztažené ke konkrétnímu typu úloh, byť se na poli IT snažíme jako lidstvo vybudovat tzv. obecnou AI, tj. AGI - Artificial general intelligence). Proto probereme postupně ty regresní modely, které mohou být do budoucna smysluplné a dají se s přijatelným úsilím spočítat a naprogramovat. A probíráme je na téhle poutní cestě od nejjednodušších po nejsložitější. Z tohoto důvodu jsem jako další volbu zvolil hyperbolickou regresi, neboť vyšší polynomy budou o dost obtížnější.

Pokud se ptáš na praktický dopad, může to být například proces, ve kterém se někdo, resp. AI, učí šachy nebo jinou hru. Nejprve se podle strmosti hyperboly bude asi rychle zlepšovat, ale pak už to zlepšování nebude tak snadné a čím bude pokročilejší, tím pomaleji se bude zlepšovat a limitně se blížit svému vrcholu (peaku). Může to být i demografická situace, která sleduje určitou míru zalidnění v konkrétním regionu. Takových jevů je v praxi celá řada.

Hyperbolická regrese - pokud jde o výpočet - je docela podobná té lineární. Budou ve výpočtech jen drobné změny. Křivka hyperbolické regrese je hyperbola. Opět půjde o 2 koeficienty A, B a pro jejich výpočet platí vzorce:

Vzhledem k tomu, že se ve vzorcích operuje s ¹/_x, je jasné, že v sadě dat X nesmíš mít nulovou hodnotu, aby nedocházelo k dělení nulou.

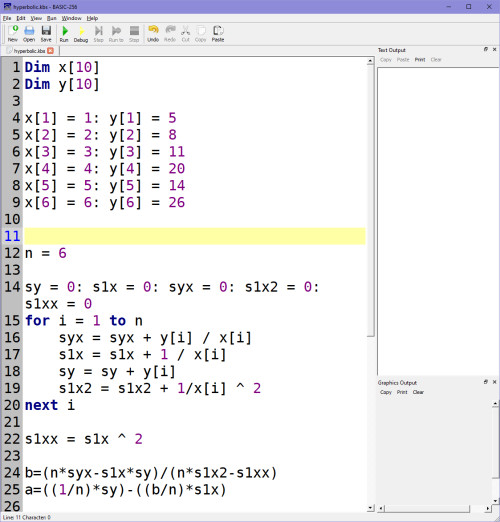
Koeficienty A, B mi vyšly takto:

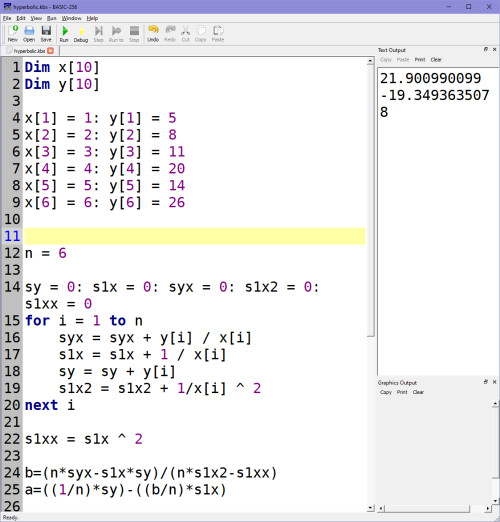
A také výsledné Y (v) bude podle vzorečku (viz výše) trochu jiné, musíme upravit:

Tím máme zkonstruovanou hyperbolu nad vstupními daty. Je to vlastně to stejné, jako když nad nimi byla přímka (lineární regrese), akorát nyní je tam křivka zvaná hyperbola, která má signifikantní zvláštnost svého ohybu.

Podíváme se na náš příklad, kde jsou vstupní data 5,8,11,20,14,26. Spustíš-li program, pak zadám-li nějaký 1000. člen v řadě, bude to jen drobná odchylka od 500. členu v řadě, zatímco odchylka 1. a 5. členu bude velká. To na základě regresní analýzy řady 5,8,11,20,14,26:

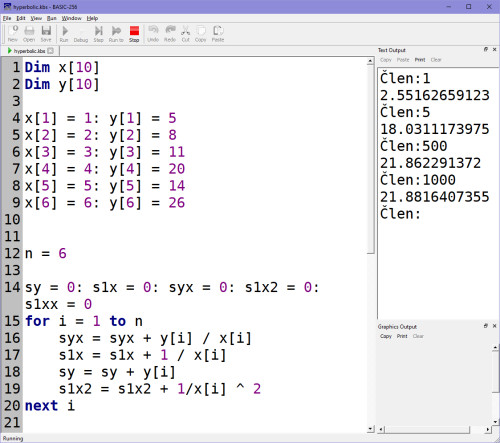
To, v čem můžeš ještě spatřovat bonus téhle regrese, je skutečnost, že ji patrně nenajdeš na kalkulačce ani ve funkcích Excelu. Máš regresní analýzu, regresní model, který není úplně obvyklý a dostupný běžnými nástroji, a jak vidíš, tak i přesto ho můžeš snadno naprogramovat, když víš jak na to. Mít ho tak ve svém arzenálu zpětných vazeb pro budoucí strojové učení.

A protože jí nikde nemáme implementovanou a nemůžeme použít nějaké automatické tlačítko, zkusíme si to, co jsme teď vypočítali, zapsat do Excelu např. pro 25 vstupních dat v intervalu 1-25. V jednom sloupci budou tedy čísla 1-25, ve druhém bude vzoreček hyperbolické regrese y = A + ^B/_x, pro který máme výsledné koeficienty

A = 21,900990099

B = -19,3493635078

Namísto proměnné X napíšeme samozřejmě buňku v Excelu, kde máme čísla 1-25:

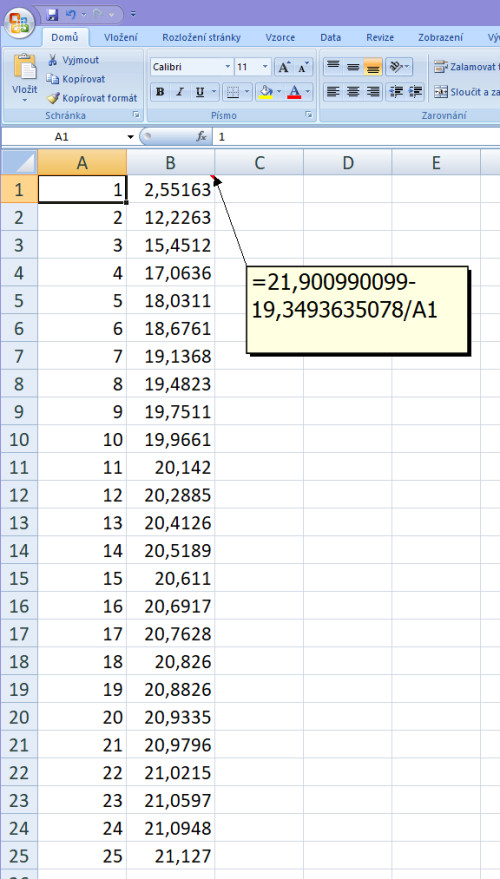
Pokud si dáme zobrazit graf nad výslednými čísly, dostaneme tento výstup v podobě hyperboly:

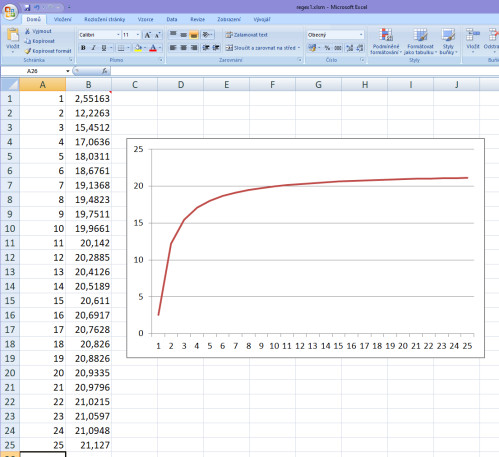
Jinými slovy vidíš, že jsme dokázali za pomoci skriptu, který vypočte koeficienty A, B pro určitou vstupní sadu dat zkonstruovat hyperbolický regresní model nad těmito daty, a se kterým můžeme dále pracovat. Zkus si třeba namísto náhodné vstupní sady 5,8,11,20,14,26 dát nějaká konkrétní čísla (třeba svou mzdu za posledních 6 měsíců) a vypočítat nad nimi hyperbolickou regresi. Dostaneš možná přesnější a zajímavější model než ti ukáže Excel ve spojnicích trendu.

<- Předchozí kapitola   Další kapitola ->