#11 Logaritmická regrese
Publikováno 05.09.2023 v 15:46 v kategorii Regrese, přečteno: 63x
Logaritmická regresní analýza (jak už jsem ti říkal v kapitole #8 Podmínky regresní analýzy) nesmí být realizována nad daty, kde se vyskytne nulová hodnota (protože logaritmus 0 neexistuje). Můžeš si takovou věc ošetřit v kódu, např. že nejprve prozkoumáš vstupní data a tam, kde je 0, tu pracovně přepíšeš na 0.00001... Vyhneš se matematické chybě a pak logaritmickou regresi udělat můžeš, ale můžeš si nadělat spousty chyb dalších (např. že atraktor křivky nebude směřovat do správného finálního stavu ap.). Takže musíš být opatrný v případě, že nulové hodnoty hrozí a je lepší se v takovém případě logaritmům vyhnout. Pokud ale nehrozí, může být tenhle druh regrese naopak velmi užitečný.
LN je přirozený logaritmus (logarithm natural), tj. o základu 2,718... V programovacích jazycích může být často vyjádřen instrukcí LOG (jak je tomu v našem skriptu Basicu-256). Vytvoříme si tedy kód, který tyhle vzorce pro výpočet koeficientů A, B zahrne. Prozatím tedy opět bez Y: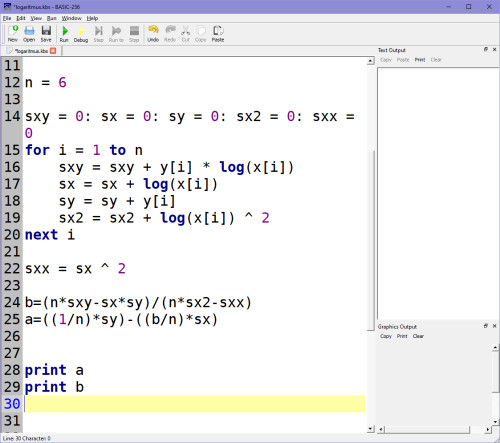
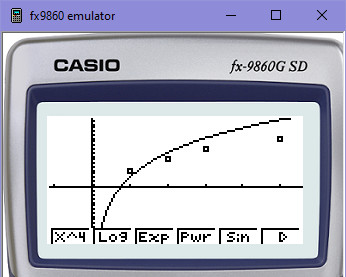
Každopádně logaritmická regrese je snadná a zase velmi podobná té předchozí, hyperbolické regresi v kapitole #10. Křivka logaritmické regrese je logaritmická křivka. Když si ji zkonstruujeme na kalkulačce, vypadá např. takhle:

Opět půjde o hodnoty 2 koeficientů A, B a pro jejich výpočet platí tentokrát tyto vzorce:
A = ((1/n) * Σy) - ((b/n) * Σ ln x)
B = (n*Σ(y * ln x) - (Σ ln x) * Σy) / (n*Σ ln x2 - (Σ ln x)2)
y = A + B * ln x
LN je přirozený logaritmus (logarithm natural), tj. o základu 2,718... V programovacích jazycích může být často vyjádřen instrukcí LOG (jak je tomu v našem skriptu Basicu-256). Vytvoříme si tedy kód, který tyhle vzorce pro výpočet koeficientů A, B zahrne. Prozatím tedy opět bez Y:

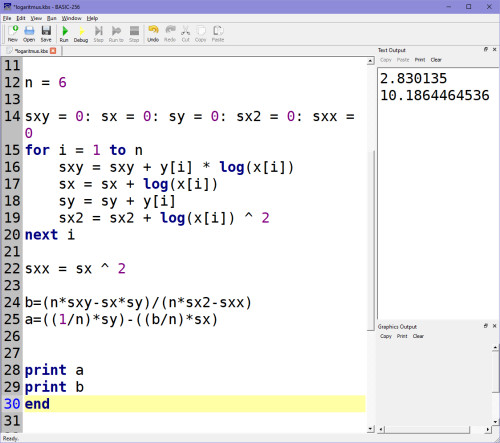
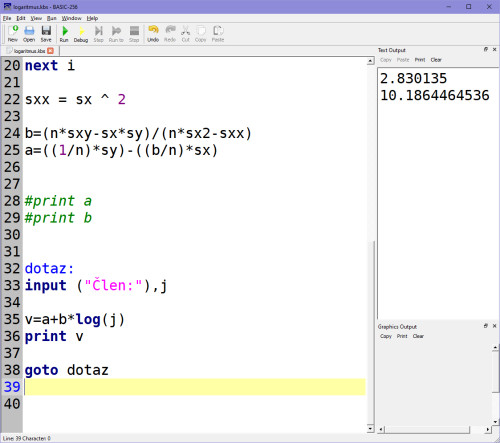
Mně vyšly koeficienty A, B pro řadu 5,8,11,20,14,26 takto, pro kontrolu:

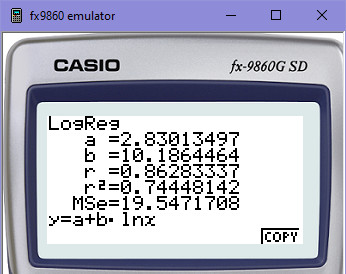
Většina vědeckých kalkulaček umí logaritmické regrese spočítat, můžeme si to tedy správnost koeficientů A, B ověřit na kalkulačce:

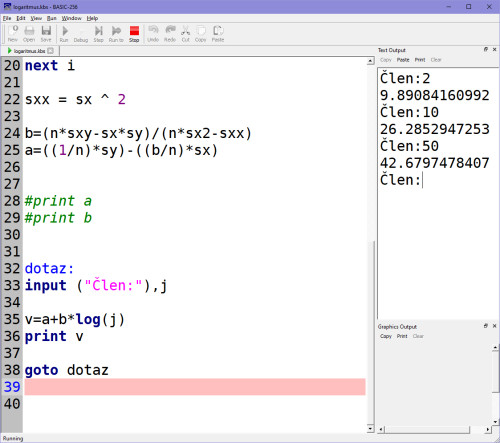
Vzorec pro výpočet Y (v) a opakování dotazu na jakýkoli člen v řadě:

Výstup logaritmické regrese na základě vstupních dat 5,8,11,20,14,26:

Jednoduchá konstrukce, jednoduchý zápis, nic více, nic méně. U logaritmů dej jen pozor, pokud budeš používat jiný jazyk než Basic-256, abys opravdu použil přirozený logaritmus, protože některé jazyky mají v základu dekadické logaritmy (a instrukcí LOG mohou vypočítávat dekadický logaritmus). To zjistíš z dokumentace k danému jazyku.
A my jdeme putovat dál. K exponenciální regresi, což je inverzní funkce k logaritmické.
Komentáře
Celkem 0 komentářů