#12 Exponenciální regrese

 Jak jsem letmo zmínil, exponenciální regrese je jen inverzní funkcí k logaritmické, takže podle toho budou vypadat i vzorce. Bude na nich drobná úprava oproti předchozí logaritmické regresi. Tam, kde byl přirozený logaritmus u X bude nyní u Y. Jde opět o výpočet 2 koeficientů A, B a vzorečky pro ně jsou:

Jak vypadá exponenciální křivka určitě víš. Existuje zase celá řada jevů, u kterých se exponenciální regresní model bude hodit. Zobrazíme si pro elementární ilustraci exponenciální křivku na kalkulačce:

My si exponenciální regresní model jako vždy naprogramujeme podle výše uvedených vzorců. Písmenko e ve vzorcích je tzv. Eulerovo číslo, což je základ přirozených logaritmů. Je to konstanta, v Basicu-256 jako instrukce EXP (např. v Pythonu je možné využít v matematické knihovně math.e), v jiných jazycích, pokud nevíš, můžeš si ji definovat sám jako konstantu e=2.71828...

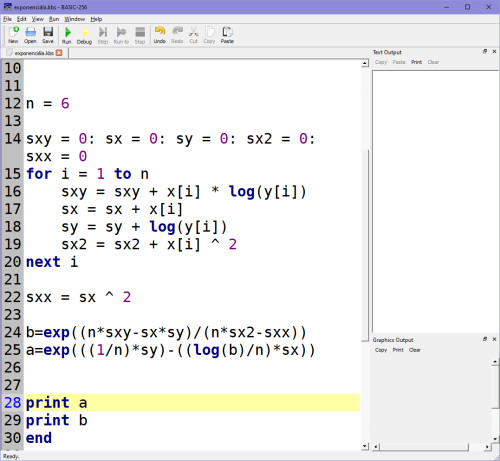
Koeficienty A, B mi vychází takto:

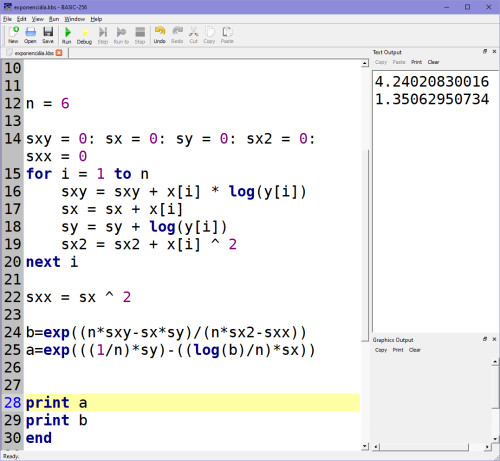
A dají se mimochodem ověřit také na kalkulačce, která disponuje regresními funkcemi. Tady jenom pozor na to, že u většiny vědeckých kalkulaček je tvar pro exponenciální regresi y = e ^ ^A+Bx, což znamená, že koeficient B bude jiný, než když požadujeme tvar y = A * B^x (tj. AB-exponenciální regrese, kde není Eulerovo číslo e). Ve výsledku je to samozřejmě to samé, ale může tě to zmást.

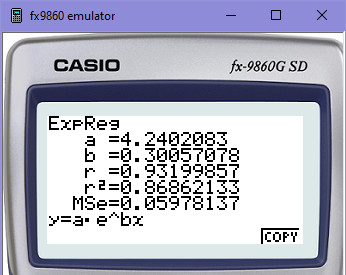
Výsledné Y (v) je podle vzorce ve skriptu pak takto:

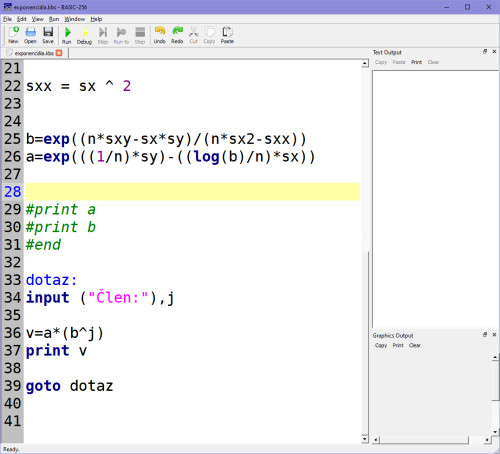
A výstupy na základě zadávání libovolných členů jsou:

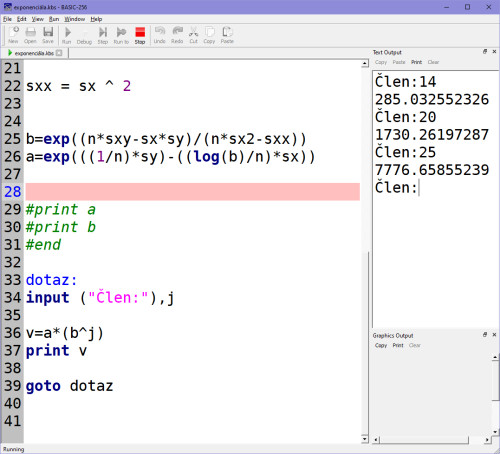
Umíš tedy sestavit exponenciální regresní model! Patří do spektra možností zpětných vazeb, které budeš mít k dalšímu programování strojového učení. Není zas tolik složité ho vypočítat a najde jistě své uplatnění. Čeká nás teď hodně podobný model a to mocninný. Věřím, že ti to brzy všechno do sebe zapadne a bude dávat smysl. Ale je třeba se těmi modely zpětných vazeb prokousat a umět je dát dohromady na elementární úrovni v nějakém programu (skriptu).

<- Předchozí kapitola   Další kapitola ->