#13 Mocninná regrese

Od exponenciální regrese se mocninná (power) odlišuje pouze minimálně. Už jen proto má smysl se ji naučit, neboť by byla škoda neumět něco dalšího, co zvedne možnosti tvých budoucích programů strojového učení a liší se to drobně od toho, co už umíš. Opět dbej podmínky, že ve vstupních datech nesmí být nulová hodnota, protože se počítá pomocí logaritmů.

U mocninné funkce je křivka poněkud variabilní. Pokud je mocnitel větší než 1 (B>1), pak to bude parabola. Pokud je tam záporný mocnitel (B<0), bude to hyperbola. Pokud je tam mocnitel B=1, bude to přímka. Existují také určité rozdíly mezi tím, zda je mocnitel (B) sudý anebo lichý. Je-li sudý, pak je funkce zdola omezená, při lichém je neomezená. Funkce nemá maximum ani minimum. Uvažujeme-li o tom, že budeme mít mocnitel kladný, tj. B>1, kde B bude přirozené číslo, pak tahle křivka bude shodná s námi už zmiňovanými polynomy - např. pokud B=2, bude to kvadratická funkce. Nicméně jak vidíš, dá se poměrně zajímavě rozšířit a přizpůsobit různým stavům, takže se nám určitě bude do budoucna hodit.

Takže křivkou mocninné funkce, kde je B>1, je mocninná křivka, v tomto případě parabola, která vypadá asi takhle:

Vzorce pro výpočet koeficientů A, B mocninné regrese jsou:

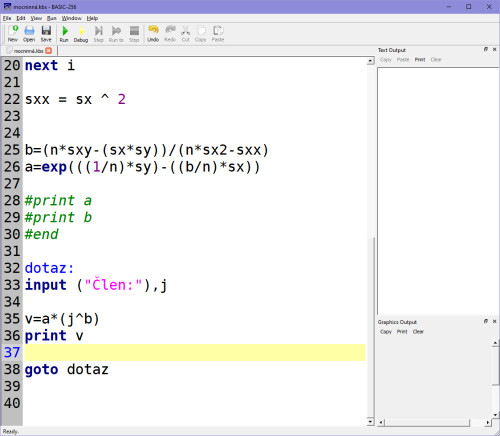
Ve skriptu bude tento výpočet vypadat nějak takto:

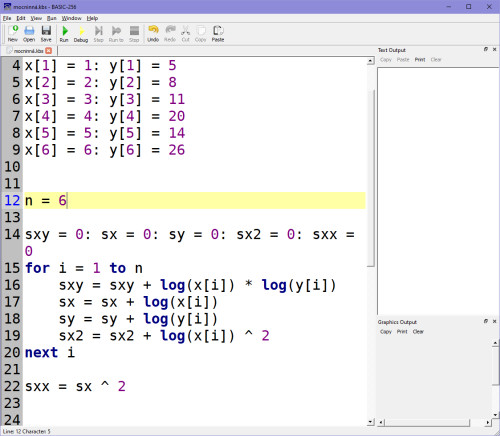
Pro kontrolu si ukažme ještě výsledek koeficientů, mně vyšly koeficienty A, B takhle:

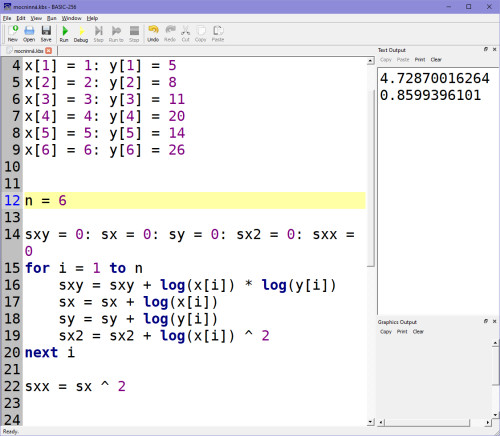
A když se podívám na kalkulačku, která většinou mocninné regrese počítat umí (na kalkulačce jsou označovány jako POWER či POW), tak tam vidím toto, na stejné řadě 5,8,11,20,14,26:

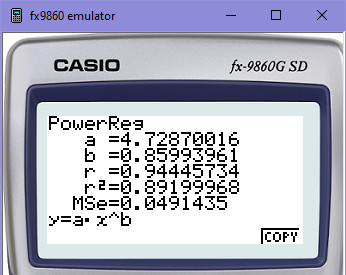
Nemůžeš si nevšimnout, že jsou ve výsledcích drobné rozdíly. Zatímco kalkulačka spočítala koeficienty na A=4.72870016, B=0.85993961, ve výstupu Basicu-256 je více desetinných míst. Je to dáno nepřesností, resp. přesností, na kterou jsem v souvislosti s jazyky upozorňoval. Přece jen výpočet koeficientů je relativně náročný a projde několika logaritmy, ve výsledku se umocňuje na koeficient B, který může být už sám o sobě nepřesný (je v něm 6 logaritmů než se spočítá). Není samozřejmě důvod k panice. Ale udělejme si spolu malý exkurz - jako by to byla myšlenková výprava do budoucnosti.

Jednou budeš programovat multiplikativní regrese, to znamená, že budeš mít celou soustavu regresních analýz v jediném spoji zpětné vazby tvé pokročilé umělé inteligence. Když se má strojové učení něco naučit, neprojde tenhle proces 1x, jako to děláme my teď a tady, na zkoušku, ale bude muset iterovat, tj. opakovat své učení řádově tisíckrát, desetitisíckrát, možná i řádově vícekrát. A pokud bude řešit komplikovanější úlohy, bude ta soustava regresí tvořit komplexní systém. A teď si představ, že nepřesnost na mocninné regresi se ti znásobí kupř. 10.000x za sekundu a v celé úloze i milionkrát. Tady je to tak nepatrné, že by se asi ještě nic nestalo. Ale přijdou ještě složitější regrese než jsou logaritmické (např. vyšší polynomy) a tam pokud bude ta nepřesnost větší, tak už to může zasáhnout do finálního rozhodování AI a její kvality. Teď otevřeme oči a nechme tenhle exkurz stranou a za námi. Nemusíš se toho teď obávat, jednou na to možná narazíš a možná ne. Ale je dobré vědět, že každá i sebemenší chybička nebo nepřesnost může akumulovat. Je dobré vědět, že nic není dokonalé, natož stroj, který provádí vyšší aritmetiku, natožpak programovací jazyk - což je také ve finále jen program.

Vraťme se k mocninné regresi. Výsledek Y (v) bude podle vzorce viz výše:

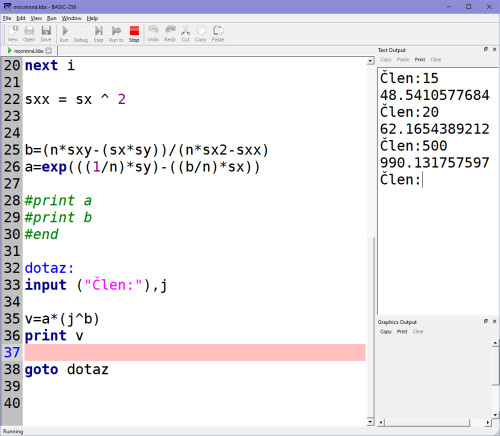
A nakonec pro kontrolu pár náhodných členů a jejich hodnoty na základě mocninné regrese:

<- Předchozí kapitola   Další kapitola ->