#15 Praktická úloha, lineární regrese 1

Ještě si pojďme chvilku pohrát s těmi regresemi, které jsme se naučili v předchozích kapitolách. Uděláme si pár příkladů, kde se taková regrese může hodit. Ber to jako procvičení, abys měl přesnější a konkrétnější představu, jak ty regrese vypadají a jak fungují. Může to být nakonec i jejich smyslem - tzn. že i tak je můžeš využívat v praxi, i když my tady, na téhle poutní cestě, směřujeme ve finále dále - k umělé inteligenci.

To, co jsme dosud nazývali vstupními daty (v souvislosti s AI se tomu může říkat tréninková data, trénovací sada), bude tvořit trajektorii křivky, mezi jakými body chceme regresi realizovat. Řekli jsme si, že výsledek každé regrese je funkce, která na základě metody nejmenších čtverců zformuje křivku tak, aby byla co nejblíže vstupním datům. Těmto vstupním datům budeme nyní říkat fixní body, resp. uzlové body.

Pro praktickou ukázku si představ trajektorii pohybu letícího motýlka mezi květy. Trajektorii bude představovat jeho let, květy jsou v našem případě uzlové body. K oné trajektorii má motýlek k dispozici pouze přímku, to znamená nemůže nikde stočit svůj směr, ale musí se nasměrovat tak, aby když poletí rovně, byl co nejblíže všem květům, které má před sebou.

Pokud má před sebou 2 květy, tj. 2 uzlové body (2 vstupní data), pak je tento úkol jednoduchý. Protože motýlek může jen nasměrovat let na první květ, směr na druhý květ a protne je oba jen přímkou.

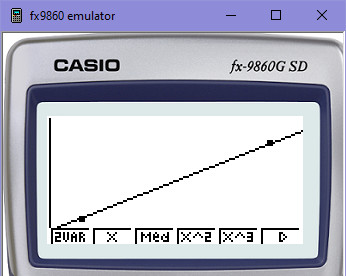
Pokud tedy chci, aby mi motýlek prolétl mezi body 1 a 2 po přímce, pak můžu použít tu nejjednodušší regresi - lineární regresi a zkonstruovat ji podle dvou uzlových bodů (vstupních dat). Nepoužijeme k tomu kalkulačku, ale náš vlastní program z kapitoly #9.

Ještě zopakuji, že zadáme do programu vstupní data polohy např.: x=1, y=100 a x=2, y=300. Podle nám už důvěrně známých vzorců spočítáme koeficienty A, B:

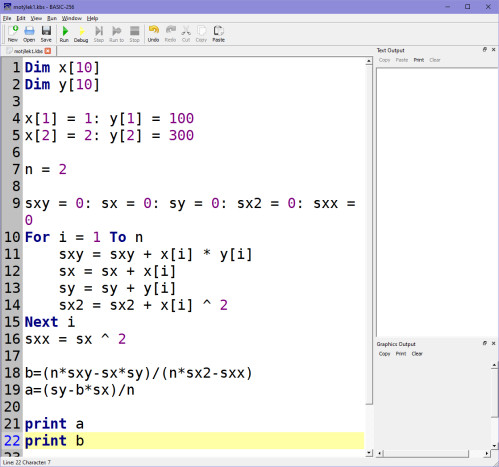
Mně vychází výsledek takto:

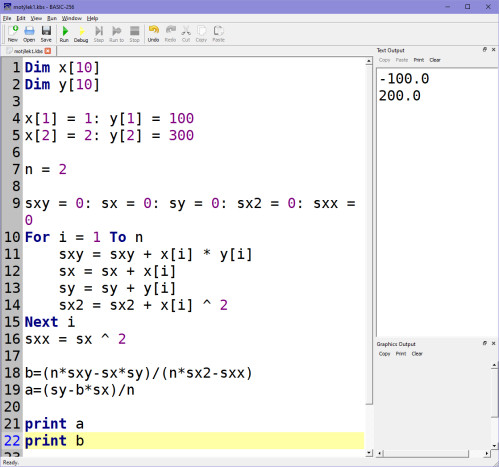
Podobný výsledek bychom dostali samozřejmě rovnou z kalkulačky, ale pro nás je podstatné, abychom regresi, tzn. koeficienty A, B, uměli spočítat sami. Můžeme ji použít ale alespoň pro kontrolu. Koneckonců na ní také vidíš, že r²=1, to znamená, že těsnost uzlových bodů k výsledné regresní přímce je rovna 1, tj. 100%. Takže motýlek, když to zjednoduším, vždy protne svým letem po přímce všechny (tj. oba) body na 100%.

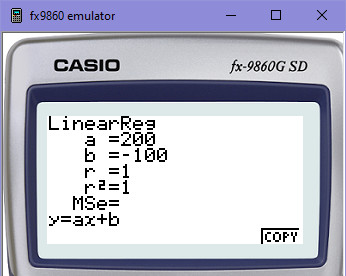
Máme tedy řešení pro lineární křivku (přímku) v podobě funkce y=A+Bx dle vzorců z kapitoly #9. A to pro 2 uzlové body, které jsme si stanovili na začátku, tzn. že chceme, aby motýlek prolétl body x=1, y=100 a x=2, y=300. Jakmile si stanovíme pohyb po ose X (to bude vždy jednoduché, protože X bude jen přibývat +1), pak nám výsledná regresní funkce bude udávat, kde se bude nacházet poloha motýlka na ose Y (dle y=A+Bx).

Tím máme hotovou jednoduchou praktickou ukázku pro lineární regresi. Můžeš si jako uzlové body stanovit jiné 2 hodnoty a dívat se, kudy motýlek prolétne, tj. jak vypadá výsledná přímková trajektorie.

<- Předchozí kapitola   Další kapitola ->