#16 Praktická úloha, lineární regrese 2

Ještě chvilku u lineární regrese zůstaneme a do prostoru si dáme více květin, tj. více uzlových bodů. Takže přímka, po které motýlek poletí, tentokráte neprotne jen 2 fixní body, kde to bylo jednoduché - a z principu je tak protne na 100% (r²=1), neboť ke konstrukci přímky jsou 2 body v prostoru definitním základem. Ale proletí např. kolem 9 bodů, kde se dostane pomocí metody nejmenších čtverců co nejblíže všem fixním bodům v prostoru. Pořád to ale bude přímka. Neboť jde pořád o lineární regresi.

Body v prostoru si dejme např. pro X, Y:

1, 100

2, 300

3, 500

4, 200

5, 600

6, 500

7, 400

8, 700

9, 600

Rozmístění uzlových bodů v prostoru bude tedy značně nesystematické a víceméně náhodné (a často kontrární, neboť vyjadřují "zájmy", kudy má nakonec motýlek letět, a tyto "zájmy" jdou proti sobě):

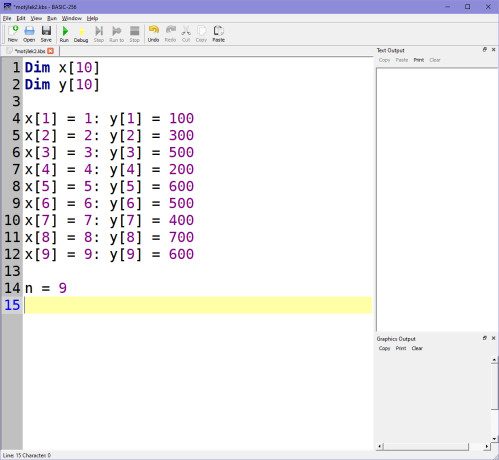
Opět v našem skriptu lineární regrese si dosadíme body X, Y a získáme výpočet pro polohu na ose Y. Nejprve tedy přepíšeme uzlové body:

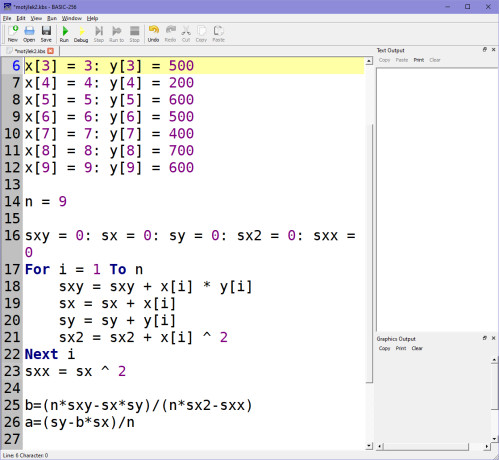
Spočítáme koeficienty A, B dle námi už známých vzorců, resp. ze známého skriptu:

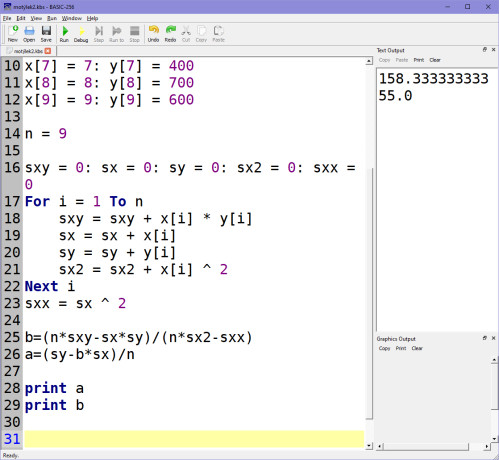
Výsledek hodnot koeficientů A, B je:

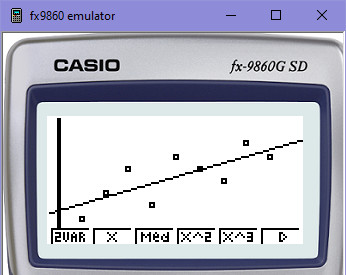
Totéž si můžeme ještě ověřit na kalkulačce, zda nám skript počítá správně:

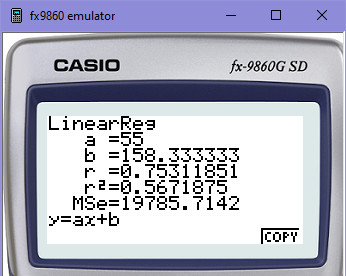
Výsledné koeficienty si dosadíme do naší rovnice y=A+Bx. Tím získáme trajektorii v podobě přímky, po které se bude motýlek pohybovat tak, aby byl - na základě metody nejmenších čtverců - co nejblíže všem uzlovým bodům. Vidíš také mimochodem, že r²=0,5671875, což znamená, že je jen asi 56,7% těsnost přímky u bodů. K pojmu těsnosti se ještě vrátíme, protože je důležitý jednak pro správný výběr regresního modelu při programování strojového učení, jednak například pro určení spolehlivosti prediktivních modelů.

Smyslem tohoto praktického a vesměs primitivního exkurzu bylo ovšem to, abys viděl, jak pomocí lineární regrese dokážeme položit přímku do prostoru tak, aby byla co nejblíže předem určeným uzlovým bodům v libovolném počtu a v libovolné poloze. A to si myslím zřejmé je a můžeš si to opět zkoušet i na svých vlastních příkladech.

<- Předchozí kapitola   Další kapitola ->