#17 Praktická úloha, hyperbolická regrese

Stejným způsobem, jakým jsme zkonstruovali lineární regresi, zkonstruujeme hyperbolickou regresi, a to na předchozí případ. Nebudeme tu dělat kapitolu po kapitole praktické ukázky všech regresí, které jsme si už v minulosti ukázali, protože stejným způsobem můžeš konstruovat i další, jen se bude měnit ten vzorec pro koeficienty A, B... a výsledné Y. Ještě tedy spolu zkusme alespoň tu hyperbolickou.

Pokud vyjdeme ze stejných uzlových bodů jako v předchozí kapitole, pak program pro výpočet koeficientů A, B pro hyperbolickou regresi bude vypadat takto:

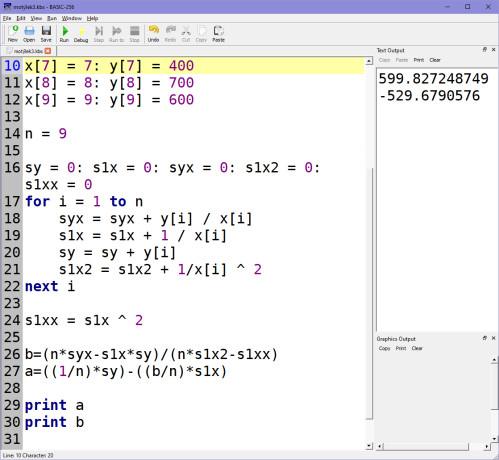
Hodnoty koeficientů A, B mi vycházejí pro kontrolu: A = 599,827248749, B = -529,6790576.

Víme, že vzorec pro Y hyperbolické regrese je Y=A+^B/_x. Můžeme ho tedy zapracovat do libovolného programu s dráhou motýlků. Motýlek tentokrát nejde po jednoduché trajektorii přímky, ale proletí mezi uzlovými body co nejblíže po trajektorii hyperboly. Obzvlášť patrné to může být vidět na začátku, kdy motýl vylétne po hyperbole a pak se už jen pozvolna přibližuje limitu.

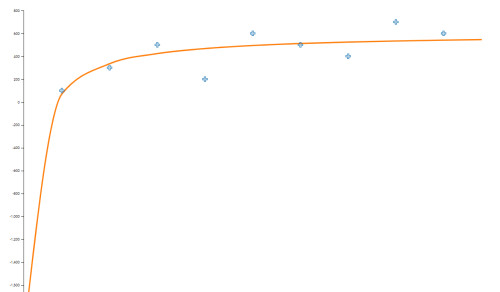
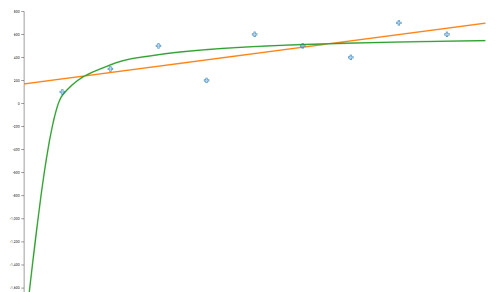
Kdybychom počítali těsnost (korelační koeficient), pak zjistíš, že u hyperbolické regrese se nám zvedl z cca 50% u lineární na více než 75%! To je výrazný posun v kvalitě regresního modelu a evidentně je pro tento případ hyperbolická trajektorie vhodnější.

Ještě pro ukázku se podívejme na přímé porovnání trajektorie průletu mezi zvolenými body za pomoci lineární a hyperbolické regrese:

<- Předchozí kapitola   Další kapitola ->