#19 Kvadratická regrese
Publikováno 22.09.2023 v 17:26 v kategorii Regrese, přečteno: 73x
Tím nejjednodušším vyšším polynomem je polynom stupně 2 - kvadratická regrese. Zdůrazňuji slovo nejjednodušším proto, že se sice dostáváme trochu výš, ale bude to naposled, co k výpočtu budeme mít hotové vzorce. Od polynomu stupně 3 už je mít nebudeme.
Křivkou kvadratické regrese (kvadratické funkce) je parabola. To znamená, že je to křivka, která má 1 zlom (ohyb). To, proč tomu tak je, jsme si už podrobně vysvětlili v kapitole #3. Obecný tvar kvadratické rovnice je Y=Ax2+Bx+C. Jak vidíš, bude zapotřebí, na rozdíl od toho, co jsme dosud dělali, určit hodnotu ne 2 koeficientů, ale 3 koeficientů - A, B, C.
Vzorce pro výpočet koeficientů A, B, C a výsledné hodnoty Y jsou tyto:
A = { [ Σ x2 y * Σ xx ] - [Σ xy * Σ xx2 ] } / { [ Σ xx * Σ x2x2] - [Σ xx2 ]2 }
B = { [ Σ xy * Σ x2x2 ] - [Σ x2y * Σ xx2 ] } / { [ Σ xx * Σ x2x2] - [Σ xx2 ]2 }
C = [ Σ y / n ] - { b * [ Σ x / n ] } - { a * [ Σ x2/ n ] }
B = { [ Σ xy * Σ x2x2 ] - [Σ x2y * Σ xx2 ] } / { [ Σ xx * Σ x2x2] - [Σ xx2 ]2 }
C = [ Σ y / n ] - { b * [ Σ x / n ] } - { a * [ Σ x2/ n ] }
Y = Ax2 + Bx + C
kde navíc:
Σ xx = [ Σ x2 ] - [ ( Σ x )2 / n ]
Σ xy = [ Σ x y ] - [ ( Σ x * Σ y ) / n ]
Σ xx2 = [ Σ x3 ] - [ ( Σ x2 * Σ x ) / n ]
Σ x2y = [ Σ x2 y] - [ ( Σ x2 * Σ y ) / n ]
Σ x2x2 = [ Σ x4 ] - [ ( Σ x2 )2 / n ]
Σ xy = [ Σ x y ] - [ ( Σ x * Σ y ) / n ]
Σ xx2 = [ Σ x3 ] - [ ( Σ x2 * Σ x ) / n ]
Σ x2y = [ Σ x2 y] - [ ( Σ x2 * Σ y ) / n ]
Σ x2x2 = [ Σ x4 ] - [ ( Σ x2 )2 / n ]
Přepíšeme si je do programu. Ale buď opatrný, aby v tom nebyla chyba. Použijeme našich známých 9 uzlových bodů z předešlých ukázek. Minimum jsou u kvadratické regrese 3 vstupní hodnoty (uzlové body, tréninková data).
Celý přepis vzorců včetně vzorců pro koeficienty do budeme mít ve skriptu takhle:
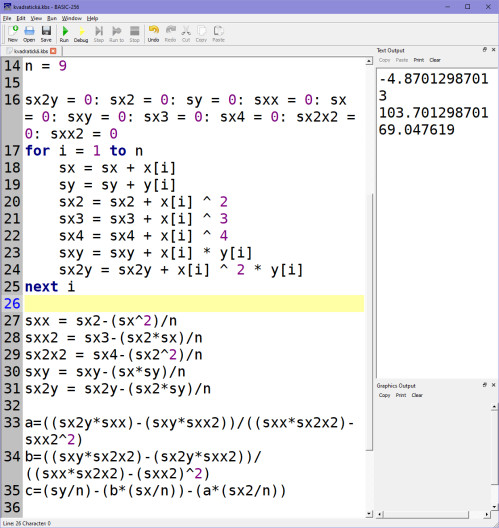
Koeficienty A, B, C pro naše uzlové body mi vyšly takto:
A = -4,87012987013
B = 103,701298701
C = 69,047619
Kvadratickou regresi si můžeme ještě ověřit na kalkulačce:
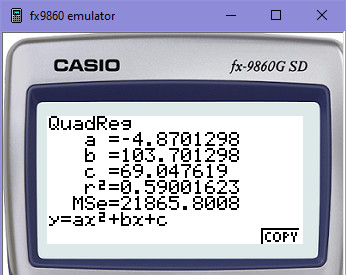
Vidíš, že máme vzorce přepsané do programu v pořádku a můžeš je tak použít pro výpočet libovolné kvadratické regrese, tj. polynomu 2. stupně. Informativně si všimni také opět hodnoty r2=0,59001623, což znamená, že přiléhavost kvadratické regrese k naší úloze je cca 59%.
Motýlek z předchozích kapitol praktických ukázek se bude tentokrát pohybovat blízko uzlovým bodům pomocí námi vypočtené kvadratické regrese, tj. po parabole. Tím máš v tuto chvíli zkonstruovanou regresní křivku 2. stupně, resp. křivku s 1 ohybem, pomocí kvadratické regrese, která za užití paraboly kopíruje optimální trajektorii mezi všemi uzlovými body, které si vymyslíš.
Komentáře
Celkem 0 komentářů