#20 Kubická regrese
Publikováno 25.09.2023 v 10:24 v kategorii Regrese, přečteno: 141x
Doposud jsme se zabývali regresemi, které se daly spočítat algebraicky, tj. za pomoci předem daných vzorečků. Od kubické regrese, tj. od polynomu stupně 3 a výše, už to tak snadno nepůjde a budeme se muset smířit s aproximací, to znamená s přibližným určením výsledku.
Připomínám, že obecný tvar kubické rovnice má 4 koeficienty A, B, C, D, které hledáme:
Ax3+Bx2+Cx+D = 0
Tady si budeme muset říct zase trochu šedé teorie, která ti umožní pochopit, jak ty vyšší polynomy konstruovat a počítat. Za prvé, budeš muset ovládnout maticové operace. Nic složitého to není, postup si osvojíš brzy, nicméně děláme to kvůli tomu, abys mohl v budoucnu sestavit polynom libovolného stupně (říkáme n-tého stupně) a spočítat ho ve vlastním programu.
Matice je v matematice nějaké schéma čísel (něco jako tabulka). Nám bude stačit docela jednoduché poskládání čísel do 2-rozměrné matice ("tabulky"), ze které potom odvodíme soustavu rovnic. Neznámé soustavy rovnic budeme počítat pomocí tzv. Cramerova pravidla. Řekneme si to bod po bodu, nejprve teoreticky v podobě postupu, v další kapitole si skript naprogramujeme.
Vše si ukážeme na naší úloze s uzlovými body z předešlých kapitol.
1. Položíme si všechny hodnoty do tabulky přehledně před sebe
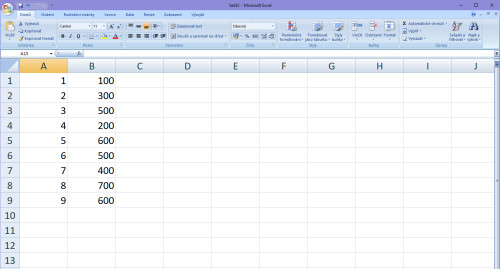
2. Sestavíme matici
Jako první číslo do matice dáme počet členů na hodnotě X. Máme tam 9 členů, tím pádem napíšeme jako první číslo 9.
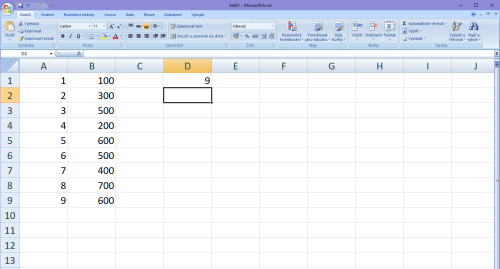
Další číslo v matici bude součet všech hodnot X. V našem případě tedy 1+2+3+4+5+6+7+8+9 = 45.
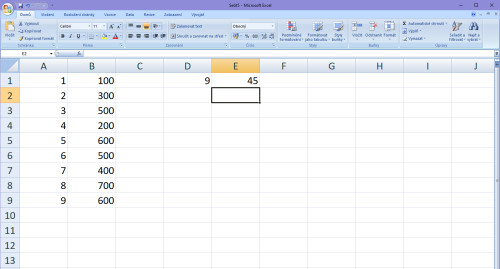
Další číslo bude součet druhých mocnin všech hodnot X. V našem případě 12+22+32+42+52+62+72+82+92 = 285.
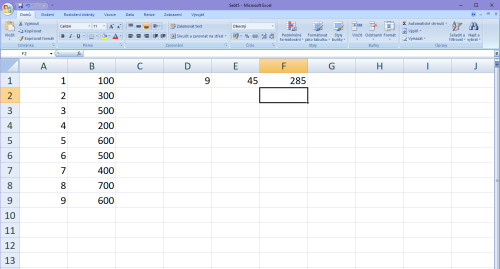
Další číslo v matici bude opět součet hodnot X, tentokráte třetích mocnin. Tedy: 13+23+33+43+53+63+73+83+93 = 2025.
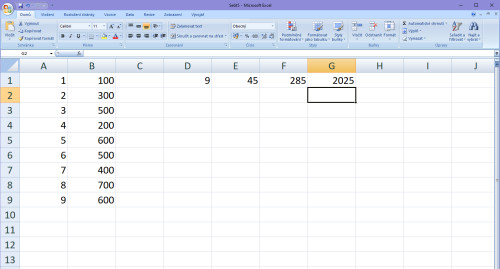
Tím máme první stranu matice, druhá pak bude počítána z hodnot Y. Doplníme si jen pro orientaci přímo do matice, že hledáme koeficienty A, B, C, D.
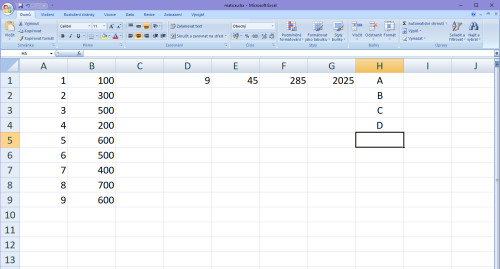
Do první buňky odshora za koeficienty, tj. do sloupce pro Y, zapíšeme prostý součet hodnot Y, v našem případě: 100+300+500+200+600+500+400+700+600 = 3900.
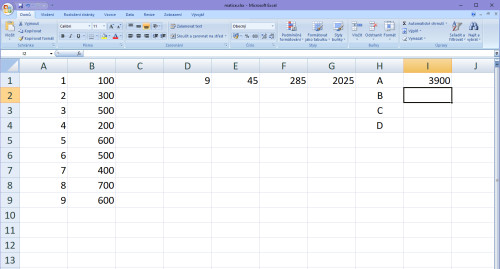
Do druhé buňky odshora zapíšeme součet součinů X a Y, v našem případě: 1x100+2x300+3x500+4x200+5x600+6x500+7x400+8x700+9x600 = 22800.
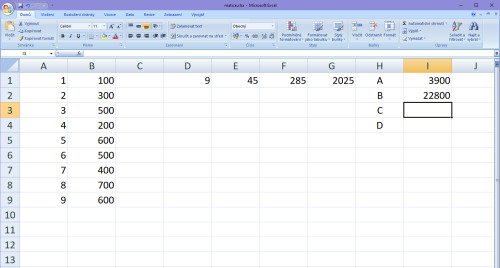
Do třetí buňka odshora zapíšeme součet součinů X2 a Y, čili to stejné, akorát X bude vždy mocnina 2. V našem případě: 12x100+22x300+32x500+42x200+52x600+62x500+72x400+82x700+92x600 = 155000.
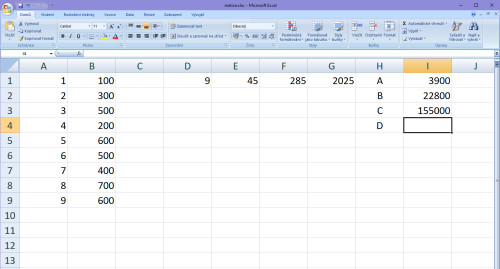
Do poslední buňky odshora v Y-části zapíšeme součet součinů X3 a Y, čili zase to stejné jako v minulém případě s tím, že namísto druhé mocniny tam bude třetí mocnina. V našem případě: 13x100+23x300+33x500+43x200+53x600+63x500+73x400+83x700+93x600 = 1144800.
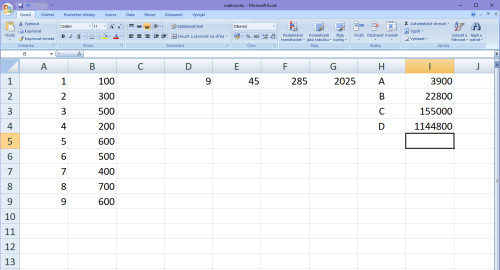
Teď doplníme tu první část matice. Dělá se to tak, že posouváme pole tak, aby posledními hodnotami začínalo a ta další hodnota bude stejná jako ta poslední s tím, že se zvedne mocnina o +1. V našem případě tedy ta druhá řádka X hodnot bude takto (přesunuté hodnoty jsem ti vyznačil zeleně):
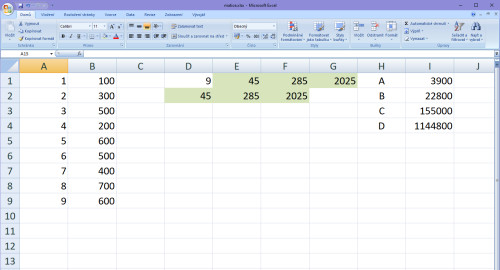
A na to poslední 4. místo, které vyšlo 2025, zvedneme jen mocninu o +1. Takže měli jsme
13+23+33+43+53+63+73+83+93 = 2025
budeme mít
14+24+34+44+54+64+74+84+94 = 15333
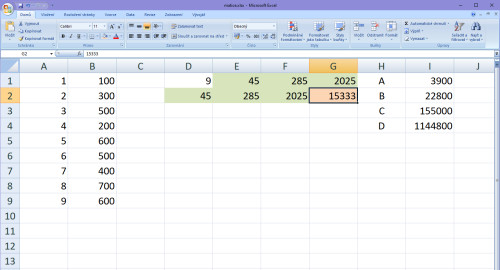
V dalším kroku uděláme to stejné do dalšího řádku, opíšeme poslední čísla, vypustíme první (abychom jakoby posouvali stále pole) a na poslední místo doplníme součet X mocnin, kde zvýšíme mocninu opět o +1. Vyznačím ten přesun a rovnou další hodnotu vzniklou z 15+25+35+45+55+65+75+85+95=120825:
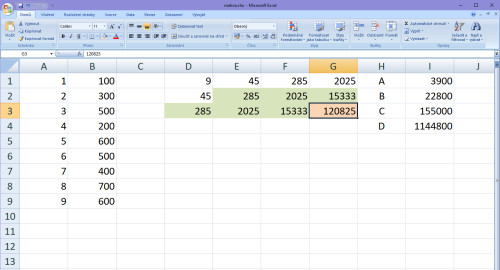
Poslední řada v X části matice bude opět posun pole, součet mocnin X, kde zvýšíme mocninu o +1, takže:
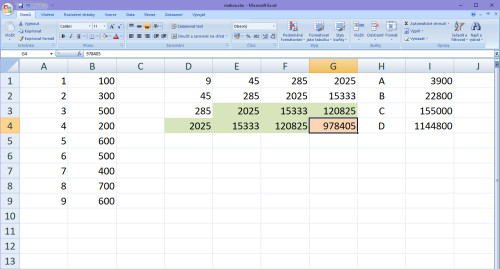
Tímto máš sestavenou matici pro koeficienty A, B, C, D kubické regrese. Doufám, že je ti jasné, jakým způsobem matici sestavíš, jak se ty mocniny v poli posouvají. Není na tom nic těžkého! Nemáš ale ještě vyhráno, neboť z té matice potřebuješ ty koeficienty dostat. Takže musíme sestavit soustavu 4 rovnic o 4 neznámých.
3. Sestavení soustavy rovnic
Rovnice se sestaví tak, že opíšeme vždycky celý řádek matice a za rovná se bude Y hodnota, která nám v matici vyšla. V našem případě budou tedy rovnice vypadat takto:
9A+10B+285C+2025D = 3900
45A+285B+2025C+15333D = 22800
285A+2025B+15333C+120825D = 155000
2025A+15333B+120825C+978405D = 1144800
Nyní je musíme vypočítat. Vypočítat soustavu lineárních rovnic lze pomocí Cramerova pravidla, což je jedna z metod numerické matematiky, při níž se určují determinanty (více na Wikipedii: odkaz ). Ale nezkomplikujme to matematickými teoriemi, i když jsou samozřejmě důležité. Protože se v nich snadno člověk utopí anebo ho můžou na dlouhou dobu nebo i nenávratně odradit. To se mně osobně stalo mockrát!
Takže si vypomůžeme a Cramerovo pravidlo nebudeme matematicky řešit, zkrátka ho jen použijeme. Já jsem našel starý program v Basicu na Atari XE/XL, v časopise VTM, který dal dohromady Ing. Karel Kulík. Je to obecně program pro řešení soustavy lineárních rovnic. Vlastně se dá říct, že to je hotový poklad!, protože máš předpřipravený skript pro řešení libovolné soustavy rovnic, tzn. pokud umíš sestavit matici - jak jsem to udělali zde, takže umíš - máš skript pro jakkoli vysoký stupeň polynomu, resp. regrese. Program funguje tak, že aproximačně (přibližně) najde za pomoci iterací (opakování) determinanty a Cramerovým pravidlem dospěje k řešení všech neznámých libovolného počtu rovnic v soustavě rovnic. Nic více, nic méně.

Teď si ho upravíme, aby nám vyhovoval. To znamená, že tam nemusí být dotazy na počet proměnných ani na známé X, Y... kteréžto hodnoty si dosadíme v programu přímo (nebo nějakým jiným než ručním vstupem). Můžeme také vypustit případ, že by soustava rovnic neměla jednoznačné řešení a budeme (naivně) předpokládat, že každý vstup našich dat mít řešení bude. Tím se nám to výrazně zjednoduší. A přepíšeme ho opět do Basicu-256. (Pokud nicméně porozumíš tomu, co jsme udělali v tom Excelu názorně, nemůže ti dělat problém naprogramovat to v jakémkoli jazyce.)
Připomínám pro pořádek, že můžeme a nemusíme zachovat strukturu programu z Atari, pokud jde o přímé skoky GOTO. Pakliže se jim chceš vyhnout nebo tvůj programovací jazyk instrukci GOTO nepodporuje, lze program přepsat do funkcí a návraty z funkcí RETURN (v každém případě to povede ke stejnému výsledku). Já se pokusím strukturu původního programu zachovat včetně GOTO, abych se příliš od vzorového programu z VTM neodchyloval.
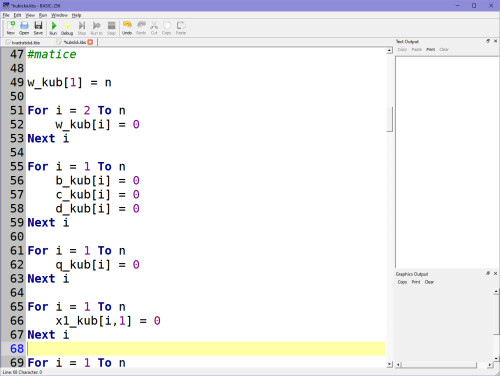
Vzhledem k tomu, že už umíš sestavit matici pro sestavení soustavy rovnic, nemusíme to zdržovat a můžeme rovnou do toho programu na začátek naprogramovat ten postup, který jsme si vyzkoušeli v Excelu (to znamená posouvání polí a umocňování). Skript nebude ve výsledku nijak složitý. Na začátku nadimenzuji pole třeba na 1000 dat (ale můžeš dle libosti tuto dimenzi měnit).
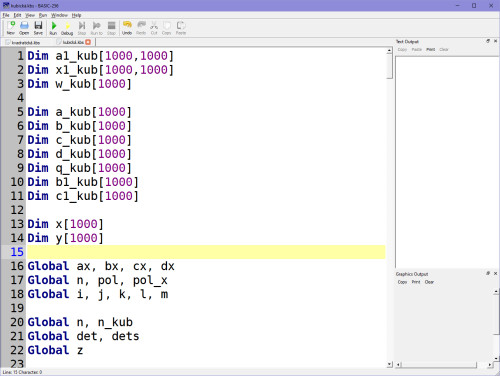
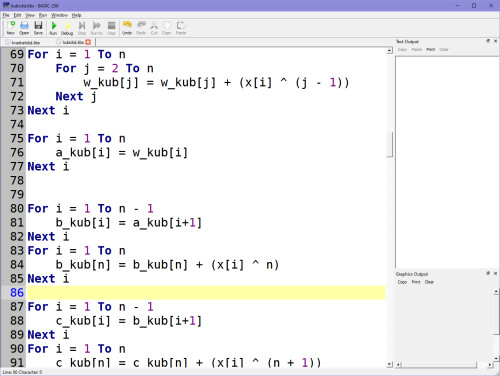
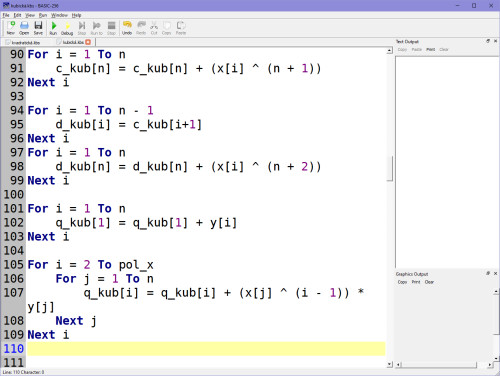
Sestavení matice podle pravidel (viz výše). Stupeň polynomu je v proměnné pol, jak jsi viděl už v matici, pracujeme pak vždy se soustavou rovnic o +1 vyšší než je polynom, což vyjadřuje proměnná pol_x. Výsledné koeficienty pak budou v proměnných ax, bx, cx, dx.
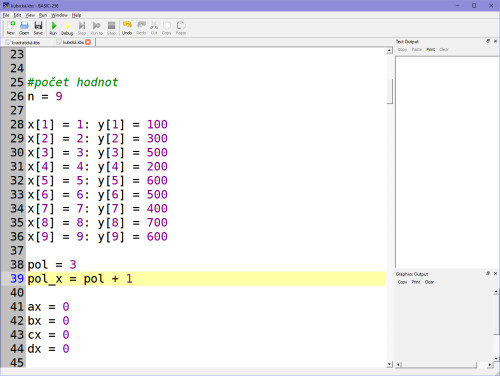
A nyní výpočet soustavy rovnic podle Cramerova pravidla (tj. přepis programu z Atari):
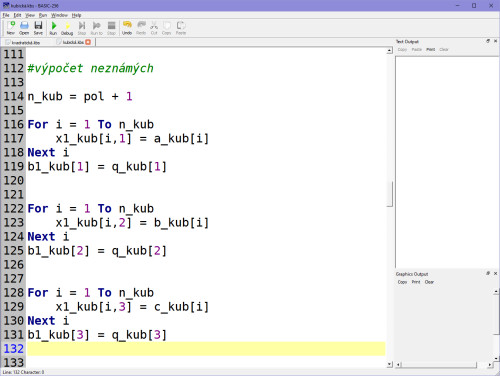
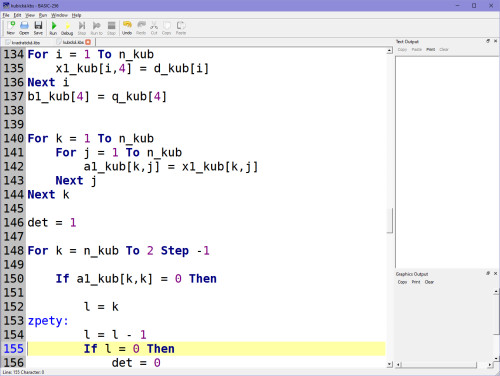
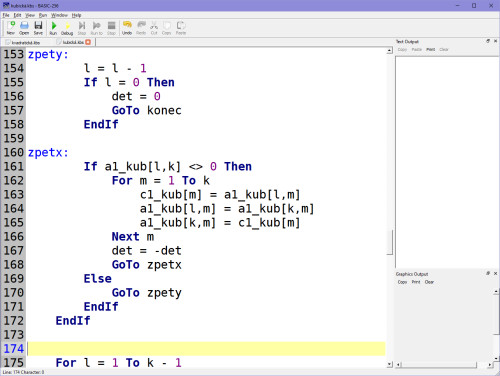
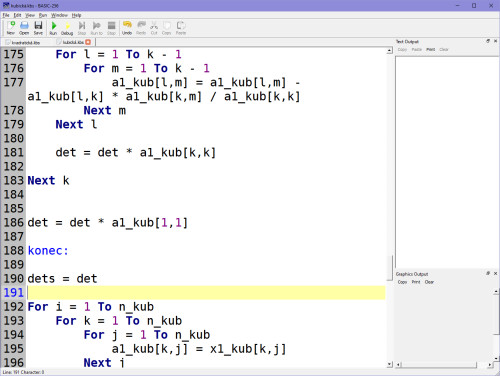
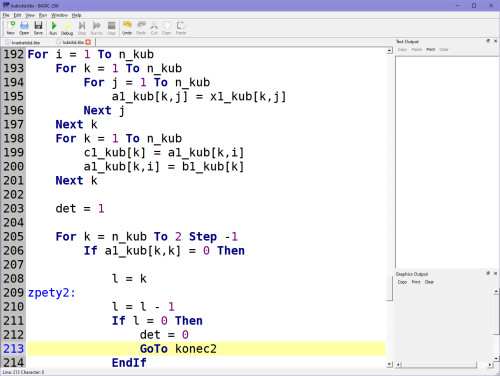
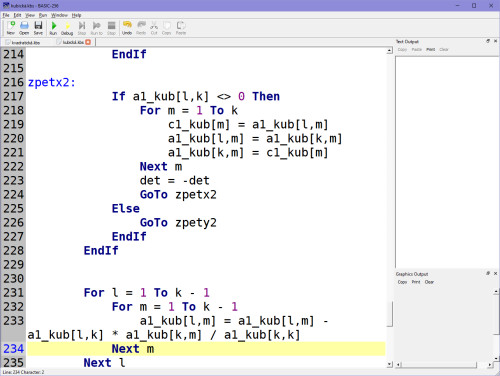
Ve výsledku, kdy se dospěje aproximačně k determinantům, zapíšeme koeficienty do proměnných ax, bx, cx, dx, což jsou naše A, B, C, D.
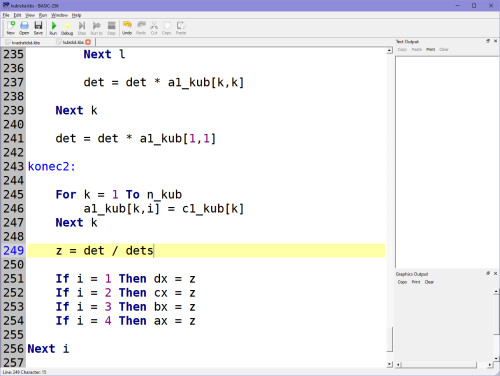
Pokud program spustíš a vypíšeš si proměnné ax, bx, cx, dx pomocí PRINT, vpravo bys měl vidět výstup - 4 hodnoty koeficientů A, B, C, D.
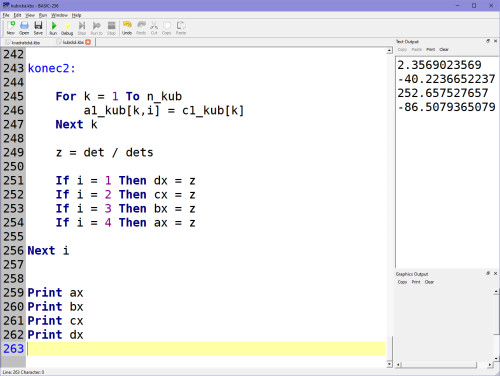
Tím jsme společně dosáhli cíle, který se možná na první pohled jeví krkolomně oproti tomu, že můžeš na kalkulačce zmáčknout tlačítko, ale onen cíl je velmi cenný, protože nejen, že už teď můžeš snadno polynom zvýšit a získat výsledky, které ti kalkulačka už nenabídne, ale také proto, že už sám jsi schopen naprogramovat zpětnou vazbu za pomoci kubické regrese!
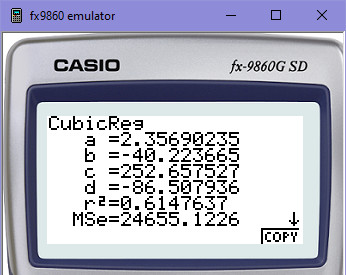
Ještě pro jistotu hodnoty ověříme s výsledkem na kalkulačce (kde opět mimochodem vidíš i hodnotu přiléhavosti r2=0,6147637, což je více než 61%).
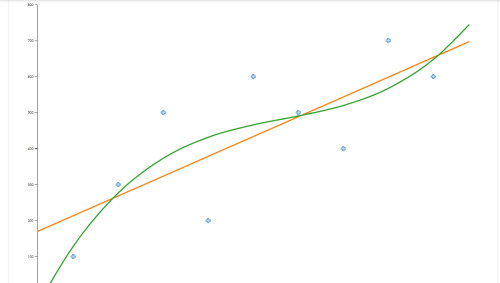
Ještě pro ilustraci, jak vypadá naše kubická regrese oproti například jednoduché lineární regresi pro tatáž data. Vidíš na ní (jak jsme si popisovali teoreticky v kapitole #3), že má 2 zlomy (tj. je to dvojitá parabola) a dostane se tak k naší datové sadě blíž (je tam vyšší těsnost, neboť součet druhých mocnin vzdáleností bodů od křivky je menši) než pouhá přímka, tj. lineární regrese.
Dovedu si představit, že tenhle přechod k polynomům pro tebe může být relativně obtížný. Ale je to pořád ještě základ před tím, než se dostaneme ke skutečnému strojovému učení. Nemyslím si - alespoň usuzuji-li ze své praxe -, že bys někdy v budoucnu potřeboval zvlášť vysoké stupně polynomů. Jednak to skýtá riziko, že s vyššími mocninami půjde ruku v ruce nepřesnost; jednak bude mít křivka tendenci atrahovat hned po proložení dat někam strmě nahoru nebo dolů (což se nám obvykle nehodí).
Obecně řečeno, vyšší polynomy se ti budou hodit spíš jako zásadní účelové funkce, například pro prediktivní modely. Ve zpětné vazbě AI je až tak nepoužiješ a vystačíš si maximálně s kvadratickou a kubickou regresí.
Přesto, když už jsme v tom, se pojďme cvičně ještě podívat na sestavení kvartické regrese, tj. regrese stupně 4. To především proto, abys viděl, jak v našem programu ty stupně regrese můžeš libovolně zvedat, resp. měnit.
Komentáře
Celkem 0 komentářů