#3 Regrese - polynomy
Publikováno 23.08.2023 v 15:30 v kategorii Regrese, přečteno: 77x
O regresích budeme teď mluvit prakticky pořád. Tady totiž platí, že čím víc druhů a způsobů provedení (konstruování) regresí budeš umět, tím to bude lepší a budeš mít více možností k programování zpětné vazby strojového učení (ML). Na to, aby se vybudovala nějaká kvalitní a silná AI, k tomu je potřeba holt trochu víc úsilí. Řeknu ti k tomu několik drobností, které se ti jednou můžou hodit.
Regrese lze spočítat snadno všude a nikde. To je ale krásné dialektické vyjádření, že?
Začněme od toho prvního, snazšího konce, tj. že je lze nalézt všude. Skoro v každé lepší kalkulačce bude určitě výpočet statistických funkcí. A mezi nimi bude funkce REG (nebo tak něco), která bude v minimální míře nabízet lineární regresi (označovanou obvykle jako X či LIN), v maximální míře nějakou exponenciální (EXP) nebo logistickou (LGST).
Regrese na kalkulačce:
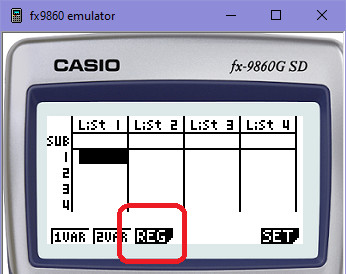
Stejně tak budeš moct např. v Excelu zobrazit u datové řady v grafu tzv. spojnici trendu, což je v českém Excelu jen jiný překlad pro regresi. Tam budou opět nějaké druhy této křivky (spojnice), končící obvykle tzv. klouzavým průměrem.
Regrese (spojnice trendu) v Excelu:
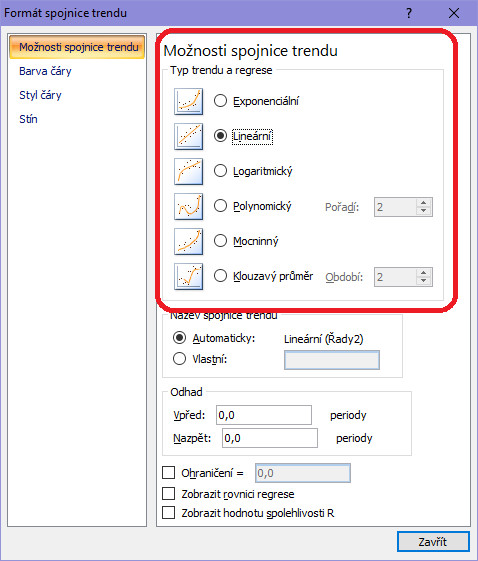
Je to hodně cizích pojmů na začátek? Já vím, chápu, ale nic není tak horoucně inteligentní, jak to na první pohled vypadá. Vezmeme to tak, aby se tomu dalo rozumět a aby to bylo hlavně k něčemu v praxi. Takže se nenechej teoretismy odradit.
V první řadě v tom uděláme pořádek, ber to jako takovou nezbytnou terminologickou hygienu ve studené vodě.
Nejprve polynomy (česky mnohočleny). Stupeň polynomu znamená nejvyšší exponent proměnné x, který se nachází v rovnici. Každý polynom tvoří nějakou křivku o počtech zlomů (ohybů). Čím vyšší polynom (polynom vyššího stupně), tím komplikovanější výpočet budeš potřebovat, ale zase tím flexibilnější AI to ve výsledku bude. Základní polynomy znáš už ze základní školy (akorát jste tomu možná tak neříkali).
- lineární regrese (polynom 1, tj. mocnina 1), dává obyčejnou přímku (0 zlomů)
- kvadratická regrese (polynom 2, tj. mocnina 2), dává parabolu (1 zlom)
- kubická regrese (polynom 3, tj. mocnina 3), dává 2 paraboly (2 zlomy)
- kvartická regrese (polynom 4, tj. mocnina 4), 3 zlomy
- kvintická regrese (polynom 5, tj. mocnina 5), 4 zlomy
- sextická regrese (polynom 6), 5 zlomů
- septimální regrese (polynom 7), 6 zlomů
- oktaviální regrese (polynom 8), 7 zlomů
- noniální regrese (polynom 9), 8 zlomů
- decimální regrese (polynom 10), 9 zlomů
Teď, v tuhle chvíli neřeš, k čemu ti to bude ve vztahu k AI, zkrátka to ber jako základní terminologii, abychom si pak rozuměli. Když někdo mluví o kvadratické funkci či rovnici, pak si můžeš představit, že je tam nějaký člen na druhou a vždy je tam počet zlomů člen-1, nebo také stupeň regrese-1, takže 1 zlom (tj. ta přímka se zlomí jen 1x, což udělá parabolu). Jinak se může stát, že někdo ty rovnice nepojmenovává a rovnou říká, že je to "polynom druhého stupně", takže ty budeš vědět, že je to kvadratická funkce. Taky se může stát, že někdo bude mluvit o "polynomu na patnáctou", tak pak už ty vyšší polynomy ani žádná jména přirozeně nemají.
Nenech se zmást tím, že jsi to třeba takhle ve škole neslyšel. Že jste možná mluvili o kvadratické funkci a kreslili si grafy. Je to to samé, v bledě modrém, kvadratická regrese je kvadratická funkce. Ve škole se akorát nemluví přímo o regresi, protože se probírá obecná matematika a o jejích aplikacích či praktických příkladech se obvykle mlčí, zatímco regresní analýza, to už je nějaká statistická aplikace.
Když jsme mluvili o tom, že výpočet regrese najdeš i na lepší kalkulačce, všimni si, že tam bude zřejmě nejvyšší polynom 4. Je to proto, že výpočty vyšších polynomů jsou komplikované i náročné na přesnost. Excel zvládne nejvyšší polynom 6 (tzn. sextickou regresi, počet zlomů křivky bude tedy stupeň regrese-1 = 5). Proč si všímáme těch zlomů, to ti ještě řeknu, vydrž...
Polynomy na kalkulačce:
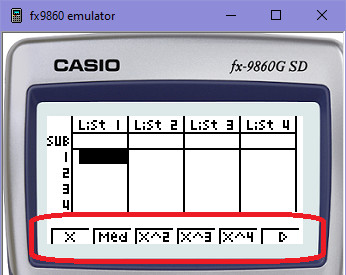
To byly polynomy (mnohočleny) - alespoň doufám - trošku přehledně. Základní rovnice a křivky regresní analýzy. V další kapitole se podíváme ještě na další rovnice a křivky, které nejsou polynomy - ale určitě je budeš znát.
Komentáře
Celkem 0 komentářů