#5 Atraktory, těsnost

Posledními pojmy, na kterých si něco o regresích ještě řekneme, jsou atraktor a těsnost. Jsou to matematické principy, které ale nemusíš až tak do detailu řešit. Pokud máš programovat svoji vlastní AI, tak ti spíš mají pomáhat k základní orientaci v problému, než aby ti ho komplikovaly.

Atraktor obecně znamená to, co se přitahuje, nějaký "přitahovač". Je to finální stav toho, kam dynamický vývoj v čase směřuje. Pokud mluvíme o křivce (např. křivce polynomu), tak atraktorem bude zkrátka jen to, zda je křivka stoupající nebo klesající, čili kam křivka ve finále směřuje - nahoru nebo dolů, tzn. kam jí to přitahuje. Např. kdybychom se podívali na vývoj počtu obyvatel v Praze, tak bez ohledu na to, jak vypadá konkrétní polynomiální křivka toho vývoje v čase, vidíme, že jde nahoru (lidí přibývá), čili atraktor je dejme tomu 1. Kdybychom se podívali na vývoj počtu obyvatel Ostravy, tak zase bez ohledu na to, jak vypadá konkrétní polynomiální křivka toho vývoje, vidíme, že jde dolů (lidí ubývá), čili atraktor je dejme tomu -1 (nevolme nulu - 0, protože ta svědčí spíš o neutrálnosti, tj. že to křivku nikam nepřitahuje). Ačkoliv je takový závěr samozřejmě reálně nesmyslný, tak podle prostého lineárního vývoje a jeho atraktoru bychom mohli usoudit, že Ostrava se jednou zcela vylidní a zanikne, tzn. že to je její finální stav.

To je základní věc, kterou atraktor v orientaci problému vyjadřuje. Na jednu stranu je to triviální, na druhou stranu je to naprosto zásadní věc. Protože ve výsledku nejde o nějaké křivky, ale jde vždy právě a jedině o ten binární atraktor - zda bude 1 nebo -1. Ptáš se i ve svém životě binárně: vyléčím se nebo ne? vyhraju tuhle partii nebo ne? vyberu tu zatáčku anebo ne? bude pršet nebo ne? vyhraju loterii nebo ne? zasáhne nás meteorit nebo nezasáhne? Všechny tyhle otázky jsou pro tebe zásadnější než to, jak vypadá křivka (cesta), po které se to děje. Je to zúžení problému do binární logiky. A to právě vyjadřuje atraktor.

Ještě to řeknu polopaticky a ve vztahu k AI. Když má AI za úkol řídit auto, musí vyhodnotit situaci tak, aby atraktor byl vždy 1 k tomu danému zadání. Když bude vidět, že k tomu vede polynom č. 4, tak zvolí polynom č. 4, protože to vede k požadovanému účelu. Jako by se dívá vždycky až na konec, až do toho finále, jak vypadá atraktor, i kdyby ten polynom nebyl ideální. Může obětovat v šachu 5 figur, když bude vidět, že to je ta cesta, která vede k atraktoru 1 - tj. k vítězství. (Finálním stavem šachové partie má být vítězství.)

Těsnost. To souvisí pořád s regresními křivkami. (V literatuře se můžeš setkat s mnoha podobnými označeními či synonymy, např. přiléhavost, blízkost, koeficient determinace ap. Na kalkulačce to bude označeno jako R², tj. R kvadrát.) Ještě ti to zopakuji a přidám k tomu ten pojem těsnosti.

Modelový příklad: Máš nějaká data v Excelu - třeba svou mzdu za poslední 2 roky. Když si zmáčkneš spojnici trendu, tak uvidíš, zda se tvůj plat průběžně zvedá nebo ne. Pokud je atraktor 1, pak jde postupně nahoru, pokud je atraktor -1, tak jde postupně dolů (jak jsem řekl, to je to, co tě nakonec zajímá nejvíc, to jest ten atraktor a jak moc je stoupající anebo klesající). Asi je skoro nulová šance, že atraktor bude 0, protože to by znamenalo, že bys poslední 2 roky bral na korunu stejnou mzdu.

Pokud ta spojnice trendu bude lineární (tj. polynom 1. stupně), tak uvidíš, jak ta přímka proložila všechny tvé platy tak, aby byla co nejblíže u nich. Tomu se říká metoda nejmenších čtverců. Excel nebo kalkulačka ti to spočítá totiž sama tak, aby součet druhých mocnin vzdálenosti těch bodů od přímky byl co nejnižší. Tím dosáhne optimálního proložení bodů (tvých platů za poslední 2 roky) přímkou (či jinou zvolenou křivkou). Uvidíš také zároveň, že ty body budou pravděpodobně daleko skákat od té přímky. Zkusme si to zmáčknout na kalkulačce.

Lineární regrese (přímka, 0 ohybů křivky):

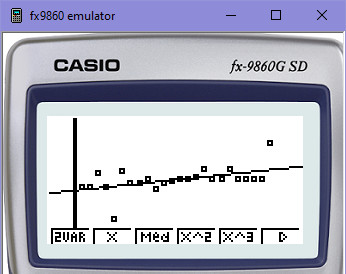
Pokud zvolíš polynom 2. stupně (kvadratickou regresi, kvadratickou funkci), tak ta parabola, která tam bude, bude o něco blíž těm bodům (platům). Pokud zvolíš 3. stupeň (kubickou regresi), tak zase ta křivka bude blíž. Pokud zvolíš 6. stupeň, tak bude určitě nejblíž. Dá se říci, že už bude prakticky kopírovat tvé platy tak, že skoro nebudou od křivky odskakovat.

Kvadratická regrese (parabola, 1 ohyb křivky):

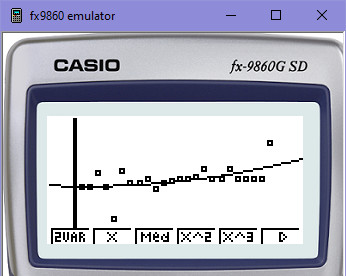
Kubická regrese (dvě paraboly, 2 ohyby křivky):

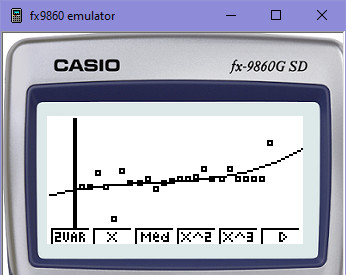
Kvartická regrese (3 ohyby křivky):

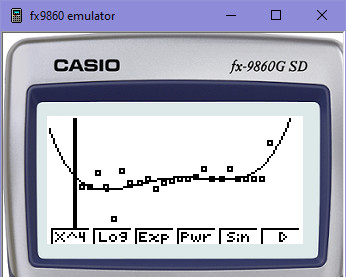
A tomuhle se říká těsnost, přiléhavost. Vyjadřuje svým způsobem míru kvality regresního modelu. Čím vyšší polynom zvolíš, tím vyšší těsnost, jak vidíš, bude. Ale jedna věc je zmáčknout si to v Excelu nebo na kalkulačce a sledovat na jednom příkladu nějaký trend vývoje či aproximaci těch křivek k bodům; druhá věc je, že musíš vzít v úvahu, že takový polynom budeš muset v případě programování strojového učení umět správně vypočítat (naprogramovat krok po kroku) a pracovat s ním v těch iteracích (smyčkách). Takže buď opatrný, protože vypočítat polynom 6. stupně bude vyžadovat vyšší matematiku, a nejen to, bude vyžadovat i přesnost výpočtů, protože mocniny 6 ti extrémně rozklíží každý výpočet, který bude zavánět jen malinkou nepřesností.

Na tomto příkladu je také zřejmé, že atraktory stahují funkci ve všech zvolených regresích nahoru, takže v praxi se plat pořád zvyšuje. Ale nemusí tomu tak být vždy. Někdy se stane, že atraktor kubické regrese půjde nahoru a kvartické dolů a obráceně. U vyšších polynomů na to dávej pozor, protože sice proloží všechny body metodou nejmenších čtverců, ale pak jakoby zbytek křivky "zahodí", aniž by atraktor byl relevantní. K tomuto problému se ale dostaneme ještě později, v souvislosti s prediktivními modely.

Takže moje průvodcovská rada: Vezmi v úvahu, že existují atraktory a těsnost. Že čím vyšší polynom, tím sice vyšší těsnost, ale taky více matematiky. Pro zpětnou vazbu v AI využij vždy jen takový stupeň regrese, který umíš bezpečně spočítat a naprogramovat! Poznej ideálně také limity jazyka, ve kterém pracuješ (tj. jak vysoký stupeň polynomu zvládne?). Pokud si nejsi jistý ani jedním ani druhým, pojďme putovat dál spolu, naprogramuješ si lineární regresi - pro začátek a pak se uvidí.

<- Předchozí kapitola   Další kapitola ->