#7 Lineární regrese, trocha teorie

Zatím jsme pořád na začátku. Slíbil jsem ti, že si zkusíme vypočítat nejprve lineární regresi. A to taky uděláme. Ale abychom úplně neodbočili z hlavní cesty a neutopili se v nějakém matematickém rašeliništi. Než začneme, připomenu ti, že každá AI má nějaký prvek zpětné vazby. To znamená to, že dokáže výsledek určité činnosti vyhodnotit a z toho, jak vypadá výsledek, se poučit, tj. překontroluje tu činnost znovu a vrátí se zase na začátek a zkusí to znovu a lépe. To "podívání se zpět" je právě regrese a "znovu na začátek", tj. opakování, je iterace (smyčka). Způsoby, jakými se "podívá zpět", jsou druhy regresní analýzy. A protože AI nemá intuici jako člověk, tak ty způsoby mohou být vesměs jen matematického charakteru, mohou to být jen matematické funkce (v programování jen funkce). A proto si o těch regresích, tj. o těch pohledech zpátky, tak obšírně povídáme.

A nyní se vraťme k tomu konkrétnímu výpočtu. Lineární regrese je, jak pořád dokola opakuji, polynom 1. stupně. Je to nejjednodušší druh regresní analýzy. Lineární model má mocninu 1 (čili jakoby neměl žádnou, protože jakékoli číslo umocněné na první je totéž číslo) a počet zlomů křivky je stupeň-1 = 0, takže se ani 1x křivka nezlomí, z čehož vyplývá, že je to přímka. Obecný tvar je Ax+B. Jinými slovy, potřebuješ se dopracovat k těm dvěma koeficientům v rovnici, tzn. k A a B.

Zkus si představit primitivní řadu čísel: 2,4,6,8,10,12... A chceš, aby AI v té řadě pokračovala. Ona to musí udělat tak, že se podívá zpátky na tu řadu (provede regresní analýzu) a na základě té se pak může doplnit další číslo. Taky vidíš jen pro orientaci, že ta řada narůstá, takže je tam atraktor 1. Dá se tedy předpokládat, že nikdy neklesne do minusových hodnot (to ti říká atraktor).

Pokud jde o lineární regresi, existují obecné vzorce. Ty jsou:

Netřeba se toho obávat, pokud to na tebe působí složitě, všechno si řekneme. Jak vidíš, tak když se počítá koeficient A, je třeba už znát koeficient B, takže nejprve budeš muset vypočítat koeficient B (jen pro pořádek).

n...je počet prvků, které máš k dispozici (v AI bychom řekli počet trénovacích dat, ale to hodně předbíhám)

Σxy suma xy...je součet násobků x a y

Σx suma x...je součet pouze prvků x

Σy suma y...je součet pouze prvků y

Σx² suma x²...je součet druhých mocnin všech prvků x

(Σx)² suma (x)²...je jen součet prvků x umocněný na 2

Ještě si dáme ty známé prvky do řady tak, abys je viděl primárně jako programátor a ne jako matematik. První prvek je 2, druhý prvek je 4, třetí prvek je 6, čtvrtý prvek je 8 atd.:

prvek 1 ... hodnota 2

prvek 2 ... hodnota 4

prvek 3 ... hodnota 6

prvek 4 ... hodnota 8

prvek 5... hodnota 10

prvek 6 ... hodnota 12

Jinak: x=1, y=2; x=2, y=4; x=3, y=6...

Nebo ještě jinak: (1,2), (2,4), (3,6)...

Vypočítej si to:

Koeficienty:

Tím jsme se dopátrali koeficientů A, B. Na kalkulačce k dispozici jsou - můžeme ověřit, ale teď už víš, jak se k nim sám dobrat. Jen pro úplnost: Údaj pod koeficienty r²=1 znamená těsnost, už jsme tenhle pojem zmínili dříve. Je to v jednotkách, takže 1=100%. Víš tedy, že těsnost (či koeficient determinace) je 100%, což znamená, že křivka, kterou jsme zvolili (lineární), proloží vstupní hodnoty na 100%, není tam žádná odchylka.

Ověření koeficientů na kalkulačce:

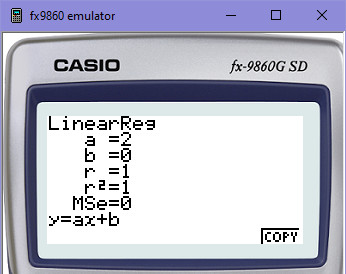
Jejich výsledek dosadíme do obecné rovnice Ax+B. Máme tedy y = Ax + B. Kdybychom měli pomocí téhle jednoduché regresní analýzy pokračovat dál v řadě, tak máme rovnici y=2*x+0, přičemž to x je kolikátý člen řady hledáme. Pokud hledáme 7. člen, máme y=2*7+0 = 14. Hledáme-li 15. člen v řadě, bude to y=2*15+0 = 30. Atd.

Můžeš jásat! Máš tu nejjednodušší formu AI, respektive strojového učení, základní zpětnovazebný systém, lineární regresi v ruce. Ještě to není smyčka v pravém slova smyslu, je to spíš jednostranný kanál, protože nemá žádné opakování. Kdybys místo řady 2,4,6... použil třeba své mzdy za poslední 2 roky, pořád už to bude fungovat a budeš to umět sám vyrobit. Tento lineární model by ti měl předpovědět, jakou mzdu budeš třeba pobírat za další rok. Nepotřebuješ najednou kalkulačku ani Excel pro výpočet koeficientů polynomu. Umíš to aritmeticky. A teď to ještě přepíšeme do programu. To už je maličkost. A nebo ne?...

<- Předchozí kapitola   Další kapitola ->