#9 Lineární regrese

Konečně se spolu podíváme na to, jak základní regresi - tj. lineární regresi, tj. polynom 1. stupně - naprogramovat. Umíš ji už spočítat aritmeticky, to znamená ne pomocí vestavěné funkce na kalkulačce. Nyní si ten postup, který jsem zmínil v kapitole #7, převedeme do programu.

Já jsem pro ukázku (jak jsem avizoval) zvolil programovací jazyk Basic-256, jehož skripty píšu ve vývojovém prostředí přímo v aplikaci tohoto nástroje. Skript Basicu je srozumitelný a dostatečně rychlý. Pokud budeš používat jiný jazyk, budou tam vždy nějaké syntaktické rozdíly a musíš tedy kód přirozeně přizpůsobit syntaxi zvoleného jazyka.

Víš, že u lineární regrese pracujeme se vzorečky pro koeficienty A, B, které pro jistotu zopakuji.

Když si vezmeme i ten stejný příklad, kdy máme v jednom sloupci pořadí členů v poli 1,2,3,4,5,6, ve druhém sloupci prvky 2,4,6,8,10,12, pak nám v kapitole #7 vyšel podle těchto vzorců výsledek:

A výsledné koeficienty:

Do kódu Basicu-256 si zapíšeme vstupní data zatím ručně:

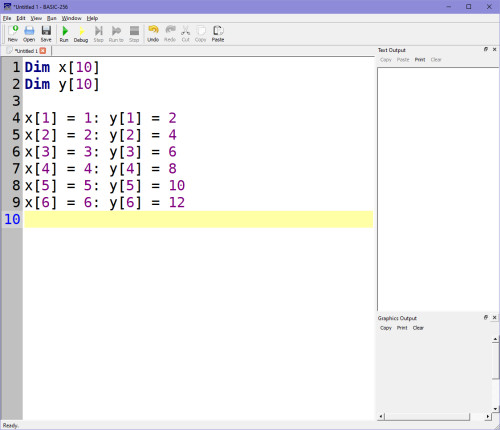
Vzorce pro sx (suma x), sy (suma y), sxy (suma xy)... si zapíšeme do cyklu FOR...NEXT tak, aby mohl být systém nezávislý na počtu vstupních dat (n=počet vstupních dat):

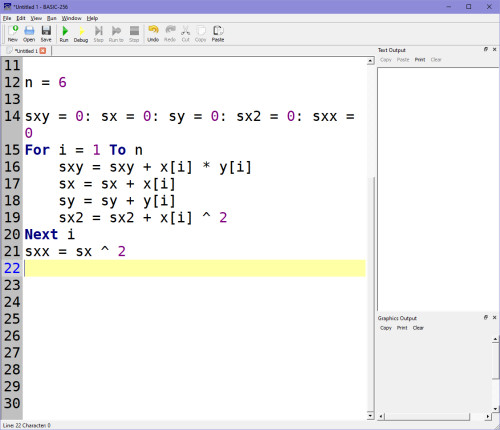
Když si vypíšeš proměnné pomocí příkazů PRINT (sxy), PRINT (sx)... 

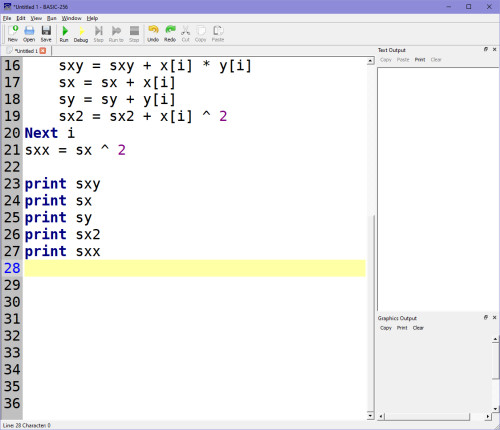
A kód spustíš (RUN), uvidíš výstup hodnot v podobě sxy, sx, sy, sx2, sxx:

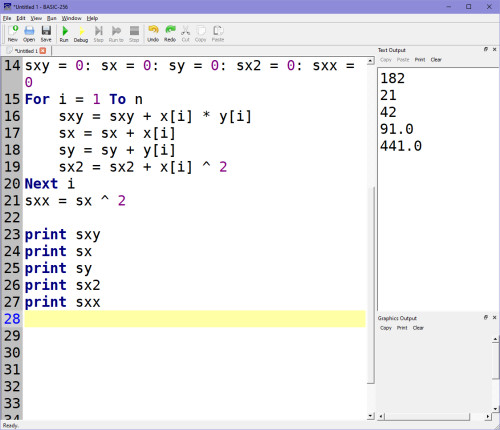
Vidíš, že se výsledek shoduje s tím, co jsme podle vzorečků vypočítali aritmeticky, čili:

Takže elementární proměnné pro výpočet regrese bychom měli mít správně. Teď už schází jen koeficienty a vzorec pro výpočet dalšího členu.

Koeficienty A, B:

V programu Basicu-256 pak zapíšeme výpočet koeficientů podle vzorce nahoře např. takhle:

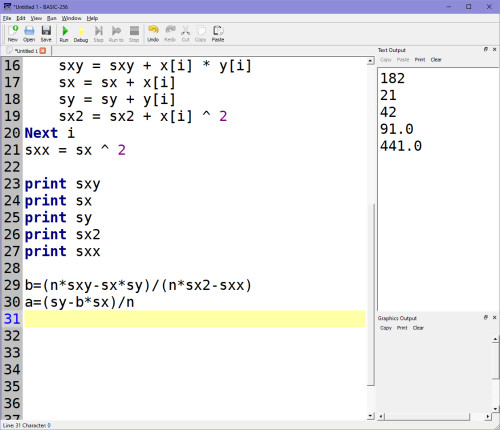
Výstup po spuštění (koeficienty A, B):

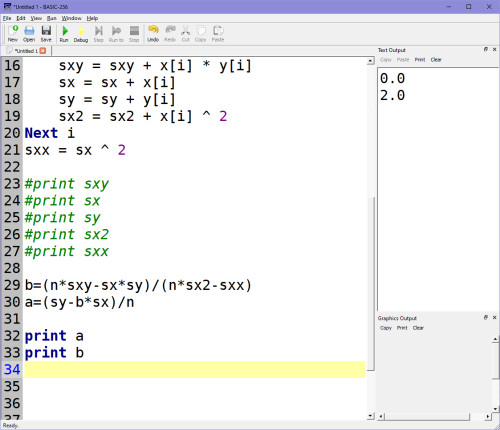
Čili koeficienty A, B máme spočítané správně. V této fázi si uděláme takový terminál na variabilní dotaz na jakýkoli člen v řadě a pokaždé se třeba k dotazu na člen vrátíme v nekonečné smyčce:

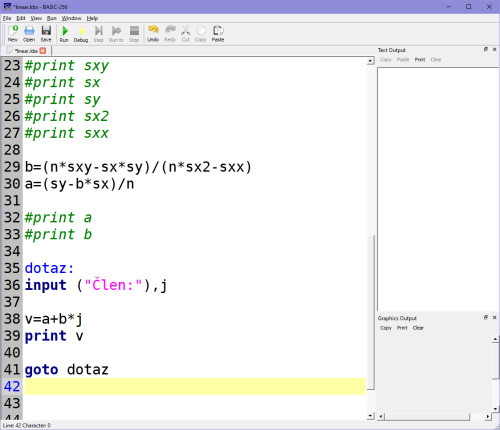
Máme tímto sestavený systém se zpětnou vazbou založenou na nejjednodušší regresní analýze 1. stupně, lineární regresi, pro libovolná vstupní data i jejich libovolný počet. Výstupem je v našem případě na onom opakujícím se terminálu tohle:

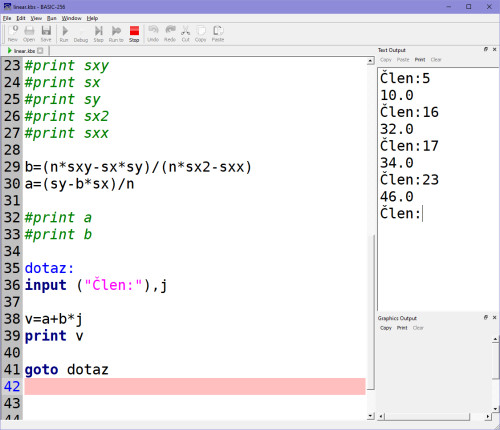
Na jakýkoli člen se zeptám, tak dostanu odpověď, jaké hodnoty bude tento člen nabývat. Mám řadu 2,4,6,8,10,12... a ptám se na 23. člen, pak je výstup 46. Atd. Je to zatím systém primitivní, pravda, nicméně funkční.

Teď pozor. Možná ti to zatím připadá jednoduché, ale budeme to přirozeně čím dál více rozvíjet a komplikovat. Ale co je hlavní: Ten tvůj systém, pokud ho máš stejně teď jako já, umí vypočítat pro libovolnou řadu koeficienty A, B a dávat pak výsledky podle zpětnovazebného výpočtu. Řada 2,4,6,8... je samozřejmě triviální. Ale zkus si tam teď dosadit nějakou jinou řadu a zeptat se na člen. Např. řadu 5,8,11,20,14,26. Uvidíš, že tvůj systém už musel aproximovat, protože ta lineární přímka, kterou tvou řadu prokládá, netrefí všechny body na 100%, ale pomocí metody nejmenších čtverců se k nim přiblíží i hypoteticky odhadne trend (tj. např. funkce v Excelu "spojnice trendu"). Výstupem je tedy:

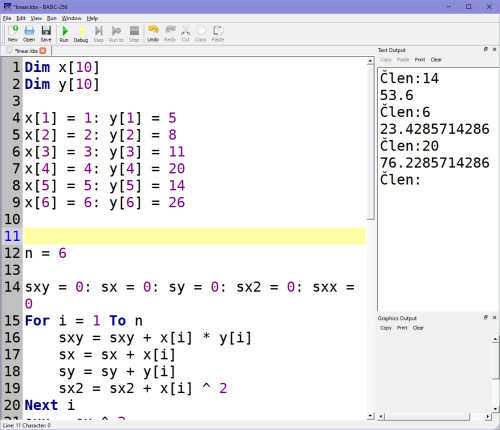
I když jsem se zeptal na 6. člen, který znám ze vstupu (= 26), tak výstup lineární regrese je 23.42857... To je zcela v pořádku, protože přímka, kterou těmito vstupními daty proložil, se nepřiblížila víc než k 23.42857, pokud se měla přiblížit i ostatním datům co nejvíce (tj. ona zmiňovaná metoda nejmenších čtverců).

Máš tedy regresi 1. stupně, nejjednodušší zpětnovazebnou křivku. Zatím bez iterací, smyček, jen řekněme "jednopohlední" zpětnou vazbu (tj. co tam strojové učení vidí na první pohled a na základě lineární regrese). Budeme samozřejmě pokračovat dál. Ale tohle si vyzkoušej, dej si tam i více dat než 6, experimentuj, jak je libo. Ale osvoj si to, abychom se pak ve vyšších polynomech neztratili a nezacyklil se nám mozek ve smyčkách.

<- Předchozí kapitola   Další kapitola ->