Regrese

Doposud jsme se zabývali regresemi, které se daly spočítat algebraicky, tj. za pomoci předem daných vzorečků. Od kubické regrese, tj. od polynomu stupně 3 a výše, už to tak snadno nepůjde a budeme se muset smířit s aproximací, to znamená s přibližným určením výsledku.Připomínám, že obecný tvar kubické rovnice má 4 koeficienty A, B, C, D, které hledáme:Ax3+Bx2+Cx+D = 0Tady si budeme muset říct zase trochu šedé teorie, která ti umožní pochopit, jak ty… Celý článek ›

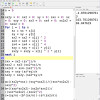
Tím nejjednodušším vyšším polynomem je polynom stupně 2 - kvadratická regrese. Zdůrazňuji slovo nejjednodušším proto, že se sice dostáváme trochu výš, ale bude to naposled, co k výpočtu budeme mít hotové vzorce. Od polynomu stupně 3 už je mít nebudeme.Křivkou kvadratické regrese (kvadratické funkce) je parabola. To znamená, že je to křivka, která má 1 zlom (ohyb). To, proč tomu tak je, jsme si už podrobně vysvětlili v kapitole #3. Obecný tvar kvadratické… Celý článek ›

Už delší dobu tě psychicky připravuji na to, že vyšší polynomy (mnohočleny) budou o něco složitější než všechny dosavadní regrese, které jsme probírali. Má to dva prosté důvody: První z nich je ten, že polynomiální křivka se dokáže vícekrát zlomit (ohnout). Druhý je, že nebude existovat jednoduché ani komplikovanější algebraické řešení pomocí už připravených vzorců, ale musí se vypočítávat pomocí aproximace.Pokud jde o to první, tj. že se… Celý článek ›

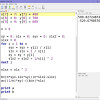
Stejným způsobem, jakým jsme zkonstruovali lineární regresi, zkonstruujeme hyperbolickou regresi, a to na předchozí případ. Nebudeme tu dělat kapitolu po kapitole praktické ukázky všech regresí, které jsme si už v minulosti ukázali, protože stejným způsobem můžeš konstruovat i další, jen se bude měnit ten vzorec pro koeficienty A, B... a výsledné Y. Ještě tedy spolu zkusme alespoň tu hyperbolickou.Pokud vyjdeme ze stejných uzlových bodů jako v předchozí… Celý článek ›

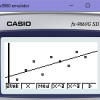
Ještě chvilku u lineární regrese zůstaneme a do prostoru si dáme více květin, tj. více uzlových bodů. Takže přímka, po které motýlek poletí, tentokráte neprotne jen 2 fixní body, kde to bylo jednoduché - a z principu je tak protne na 100% (r2=1), neboť ke konstrukci přímky jsou 2 body v prostoru definitním základem. Ale proletí např. kolem 9 bodů, kde se dostane pomocí metody nejmenších čtverců co nejblíže všem fixním bodům v prostoru. Pořád to ale bude… Celý článek ›

Ještě si pojďme chvilku pohrát s těmi regresemi, které jsme se naučili v předchozích kapitolách. Uděláme si pár příkladů, kde se taková regrese může hodit. Ber to jako procvičení, abys měl přesnější a konkrétnější představu, jak ty regrese vypadají a jak fungují. Může to být nakonec i jejich smyslem - tzn. že i tak je můžeš využívat v praxi, i když my tady, na téhle poutní cestě, směřujeme ve finále dále - k umělé inteligenci.To, co jsme dosud… Celý článek ›

Od exponenciální regrese se mocninná (power) odlišuje pouze minimálně. Už jen proto má smysl se ji naučit, neboť by byla škoda neumět něco dalšího, co zvedne možnosti tvých budoucích programů strojového učení a liší se to drobně od toho, co už umíš. Opět dbej podmínky, že ve vstupních datech nesmí být nulová hodnota, protože se počítá pomocí logaritmů.U mocninné funkce je křivka poněkud variabilní. Pokud je mocnitel větší než 1 (B>1), pak to… Celý článek ›

 Jak jsem letmo zmínil, exponenciální regrese je jen inverzní funkcí k logaritmické, takže podle toho budou vypadat i vzorce. Bude na nich drobná úprava oproti předchozí logaritmické regresi. Tam, kde byl přirozený logaritmus u X bude nyní u Y. Jde opět o výpočet 2 koeficientů A, B a vzorečky pro ně jsou:A = e ^ ((1/n) * Σ ln y) - ((ln b/n) * Σx)B = e ^ (n*Σ(x*ln y) - (Σx * Σ ln y) / (n*Σx2- (Σ ln x)2)y = A * BxJak vypadá exponenciální křivka určitě víš.… Celý článek ›

Logaritmická regresní analýza (jak už jsem ti říkal v kapitole #8 Podmínky regresní analýzy) nesmí být realizována nad daty, kde se vyskytne nulová hodnota (protože logaritmus 0 neexistuje). Můžeš si takovou věc ošetřit v kódu, např. že nejprve prozkoumáš vstupní data a tam, kde je 0, tu pracovně přepíšeš na 0.00001... Vyhneš se matematické chybě a pak logaritmickou regresi udělat můžeš, ale můžeš si nadělat spousty chyb dalších (např. že atraktor… Celý článek ›

Vrhneme se na hyperbolickou regresi... "Proč, proboha, na hyperbolickou regresi?!" říkáš si asi teď. Tak ještě jednou, pro zopakování. Regresní analýza je základní zpětnovazebný mechanizmus strojového učení a potažmo v obecné rovině umělé inteligence. Čím širší spektrum regresí budeš znát a umět je naprogramovat, tím flexibilněji budeš moct realizovat úlohy, které bude mět tvoje AI řešit. Nikdy dopředu nevíš, jaká regrese se ti bude hodit a ani já ti… Celý článek ›